
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Основные формулы для определения тесноты связи
|
|
| № п/п | Показатель | Формула расчета | Что показывает данная величина |
| Линейный коэффициент корреляции (при прямолинейной связи) |
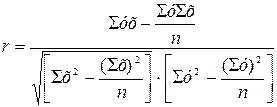
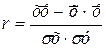
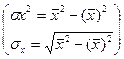
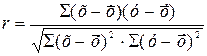
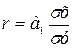 (если вычислен коэффициент регрессии (если вычислен коэффициент регрессии 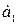 ) )
| Тесноту связи от 0 до 1 Шкала Чеддока: r = 0 – связь отсутствует, r =0, 1-0, 3 – связь слабая, r =0, 3-0, 5 – связь умеренная, r =0, 5-0, 7 – связь заметная, r =0, 7-0, 9-связь высокая r =0, 9-0, 99 –связь весьма высокая, r =1, 0-связь полная, функциональная | |
| Эмпирическое корреляционное отношение (при криволинейной связи) | 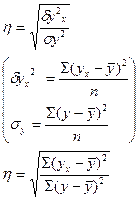
| Тесноту связи от 0 до 1 | |
| Коэффициент детерминации (подкоренное выражение) |
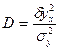
| Долю вариации результативного признака под влиянием вариации признака–фактора | |
| Множественный коэффициент корреляции |
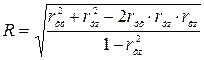
| Тесноту связи от 0 до 1 между тремя факторами (х, у, z) | |
| Индекс корреляции |
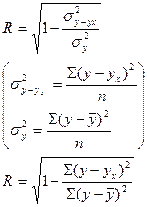
| Тесноту связи от 0 до 1;
 - характеризует вариацию результативного признака под влиянием прочих неучтенных факторов. - характеризует вариацию результативного признака под влиянием прочих неучтенных факторов.
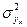 - характеризует вариацию результативного признака под влиянием всех факторов. - характеризует вариацию результативного признака под влиянием всех факторов.
| |
| Коэффициент корреляции рангов (для ранжированного ряда по значению признака х). Коэффициент Спирмена |
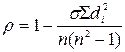
| Тесноту связи от +1 до –1. Если p = 0 – связь отсутствует. При прямой связи коэффициент p – положительная правильная дробь. При обратной связи коэффициент p – отрицательная. |
Литература
1. Статистика: учебник / под ред. И.И. Елисеевой. – М.: Высшее образование, 2009.
2. Статистика: учебное пособие / В.Н. Салин, Э.Ю. Чурилова, Е.П. Шпаковская. – 3-е изд. стер. – М.: КНОРУС, 2009.
3. Общая теория статистики: учебник / под ред. О.Э. Башиной, А.А. Спирина. - 5-е изд., доп. и перераб. – М.: Финансы и статистика, 2007.
4. Общая теория статистики: учебник М.Р. Ефимова, Е.В. Петрова, В.Н. Румянцева. – М.: Инфра, - М., 2004.