
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Теория подобия.
|
|
Подобие в широком смысле – это возможность распространения результатов экспериментов с модели на оригинал. В узком смысле подобие – это тождественность описания полей соответствующих величин модели и оригинала в обобщённых переменных или, по-другому, постоянство отношения сходственных величин модели и оригинала. Далее «подобие» будем понимать в узком смысле.
Подобные объекты описываются одной системой дифференциальных уравнений и имеют подобные условия однозначности (геометрическое подобие, временное подобие, подобие физических величин, подобие начальных и граничных условий).
Геометрическое подобие – постоянство отношения всех сходственных линейных размеров модели и оригинала.
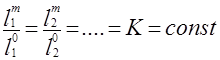 , (2.88)
, (2.88)
где l и l – сходственные линейные размеры модели и объекта, K – константа геометрического подобия.
Временное подобие (гомохронность) – постоянство отношения сходственных интервалов времени модели и оригинала:
 , (2.89)
, (2.89)
Если 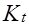 =1, то имеем синхронность.
=1, то имеем синхронность.
Подобие физических величин - постоянство отношения физических величин для модели и оригинала в сходственных точках сходственного момента времени:
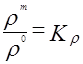 ,
, 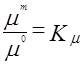 ,
, 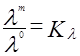 (2.90)
(2.90)
Подобие модели и объекта предполагает подобие полей физических величин:
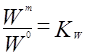 - гидродинамическое подобие (подобие полей скоростей)
- гидродинамическое подобие (подобие полей скоростей)
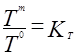 - тепловое подобие (подобие полей температуры)
- тепловое подобие (подобие полей температуры)
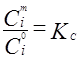 - концентрац. подобие (подобие полей концентраций)
- концентрац. подобие (подобие полей концентраций)
При соблюдении геометрического и временного подобия будет соблюдаться также подобие полей скоростей, температур, концентраций и других физических величин.
Подобие начальных условий – подобие полей всех физических величин в начальный момент времени.
Подобие граничных условий – постоянство отношения соответствующих величин на границах модели и оригинала.
Константы подобия – отношения одноимённых величин модели и оригинала. Они постоянны для различных сходственных точек подобных систем.
Инварианты подобия – безразмерные отношения величин, характеризующих модель или оригинал.
Симплексы подобия – инварианты подобия, представляющие собой отношения однородных величин:
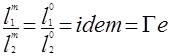 (2.91)
(2.91)
Критерии подобия – инварианты подобия, представляющие собой отношения разнородных, сложных величин. Например:
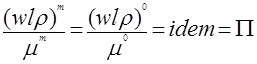 (2.92)
(2.92)
Определяющие критерии подобия составлены из величин, входящих в условия однозначности. Определяемые критерии подобия содержат величины, которые необходимо определить.
Наиболее простой метод получения критериев подобия заключается в следующем: дифференциальное уравнение приводится к безразмерному виду делением всех членов на один из них. Полученные комплексы являются критериями подобия.
Теоремы подобия:
1. Подобные объекты характеризуются численно равными критериями подобия.
2. Решение дифференциального уравнения (уравнений) описывающего объект, может быть представлено в виде зависимости между критериями подобия.
3. Объекты подобные, если они описываются одной системой дифференциальных уравнений, имеют подобные условия однозначности и их определяющие критерии равны.
Математическая зависимость между критериями и симплексами подобия, характеризующими данный процесс переноса субстанции, называется критериальным уравнением:
 (2.93)
(2.93)
Если определяемый критерий, то имеем:
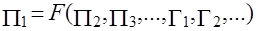 (2.94)
(2.94)
Лекция 4 Подобие гидродинамических, тепловых и массообменных процессов. Основные критерии подобия