Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Методика выполнения Задания № 7
|
|
«Задача о назначениях. Оптимизационное моделирование»
Задача о назначениях - частный случай транспортной задачи. Такая задача решается при определения маршрута передвижения людей, автомашин; при распределении людей на работы, должности; при распределении групп по аудиториям и т.д.
Условия задачи:
Имеется n городов. Выехав из одного из них, коммивояжер должен объехать все и вернуться в исходный город. В каждый город можно заезжать только один раз, и, следовательно, маршрут коммивояжера должен образовывать замкнутый цикл без петель (например, если есть 6 городов 1, 2, 3, 4, 5 и 6, то 1 - 4 -2 - 1 и 3 - 5 - 6 - 3 - подциклы (петли). Требуется найти кратчайший замкнутый маршрут коммивояжера, если известна матрица расстояний между городами1.
Математическая модель
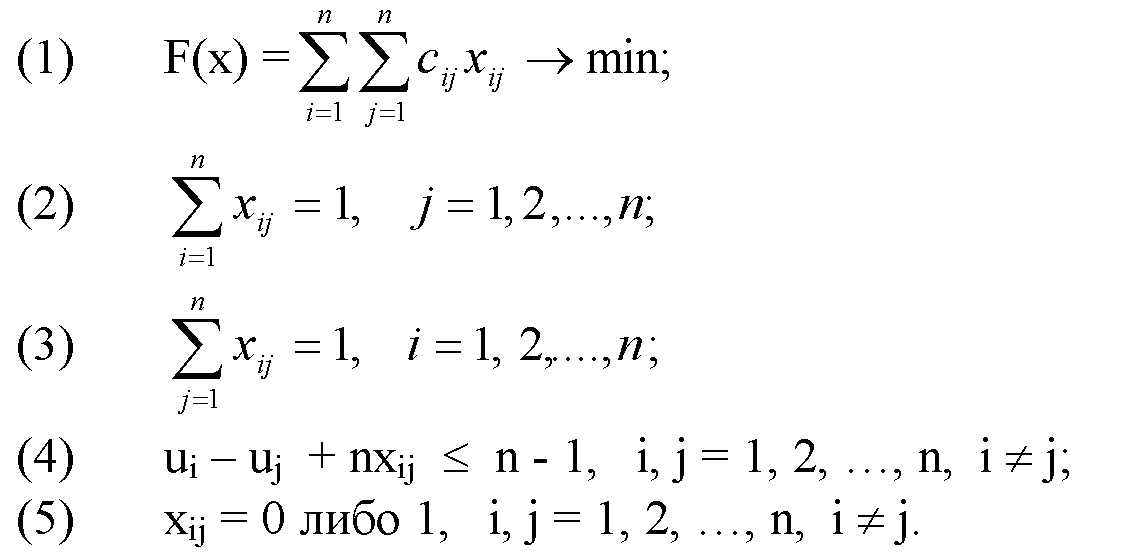
|
Здесь переменная xij принимает значение 1, если коммивояжер переезжает из города i в город j
(i, j = 1, 2,..., n, i ≠ j) и 0 в противном случае. Условие (1) представляет собой оптимизируемую функцию, где cij расстояние между городами (i, j = 1, 2,., n, i ≠ j), причем, в общем случае cij ≠ cij; условие (2) означает, что коммивояжер выезжает из каждого города только один раз; (3) - что он въезжает в каждый город только один раз; (4) обеспечивает замкнутость маршрута и отсутствие петель, где ui и uj - некоторые вещественные значения i, j = 1, 2,..., n, i ≠ j.
Постановка задачи:
Имеется 6 пунктов. Коммивояжер должен посетить их по одному разу и вернуться в исходный город. Найти кратчайший маршрут. Расстояния между городами заданы в виде матрицы чисел, представленной в Таблице 1:
Таблица 6. Вариант задания №1. Матрица расстояний между городами.
| - | |||||
| - | |||||
| - | |||||
| - | |||||
| - | |||||
| - |
Выполнение задания:
1. Первым шагом выполнения задания было ввод исходных данных в MS Excel следующим образом:
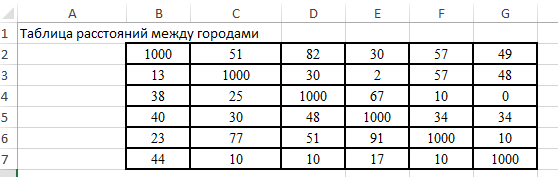
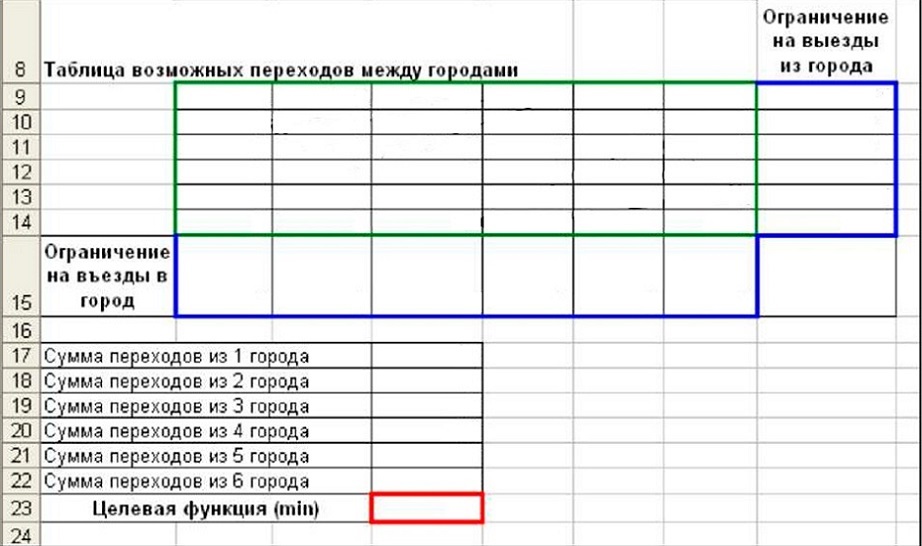
Рисунок 4. Фрагмент рабочего листа исходных данных и ограничений
· Диапазон ячеек B2: G7 содержит исходную матрицу расстояний между городами, в которой расстояние от города до самого себя приняты достаточно большими, по сравнению с другими расстояниями (например, 1000). Данный прием замены нулевых расстояний на бесконечные используется в классическом методе «ветвей и границ» решения задач данного типа с целью заранее исключить из решения нулевые по расстоянию переходы, которые хотя и являются наикратчайшими, но не допустимы по смыслу задачи.
· Диапазон ячеек B9: G14 предназначен для плана возможных переходов между городами, который будет получен в результате решения задачи.
· В ячейках B15: G15 и H9: H14 находятся формулы расчета количества въездов и выездов из городов
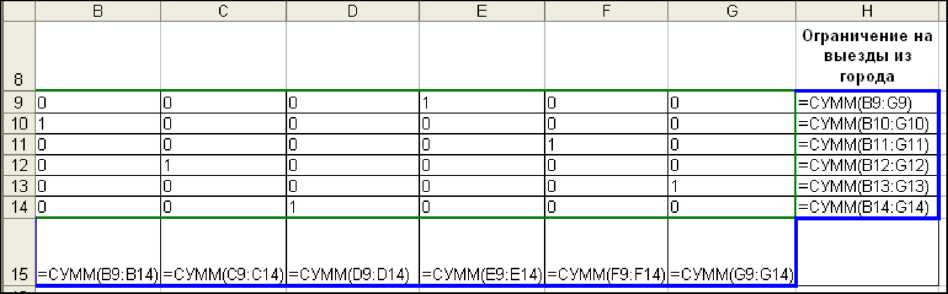
Рисунок 4. Фрагмент рабочего листа исходных данных и ограничений
· В ячейке D23 - целевая функция, использующая вспомогательные промежуточные расчеты блока D17: D22
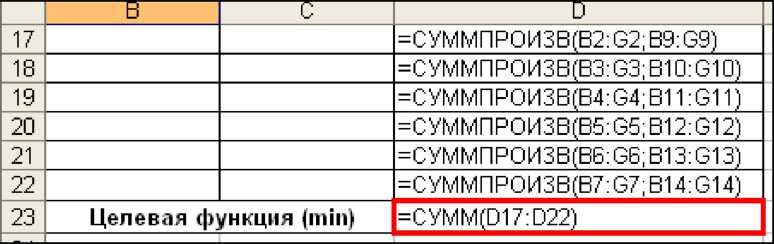
Рисунок 5. Фрагмент рабочего листа исходных данных и ограничений
2. Следующим шагом был выполнен поиск решения, используя ограничения:
Таблица 7. Ограничения к заданию 7.
| Поле «Ссылка | Тип | Поле | Примечания |
| на ячейку» | ограничения | «Ограничение» | |
| $B$15: $G$15 | = | Ограничения на въезды - условие (2) | |
| $H$9: $H$14 | = | Ограничения на выезды - условие (3) | |
| $B$9: $G$14 | = | двоичное | Условие(5) |
3. Результат выполнения поиска решения - на Рис. 5.
При упорядочении найденного решения получаем, что в качестве оптимального плана данной задачи найдены две цепочки (петли) переходов. Следовательно, найденное решение не удовлетворяет условиям задачи ввиду наличия в нем подциклов (петель). Было введено дополнительное ограничение, исключающее наличие найденных в плане петель. Для этого выполнены следующие действия:
• В любой ячейке, например, D25 подсчитана сумму найденных переходов
= CУMM(E9; B10; F11; C12; G13; D14), которая равна 6.
• Проведен повторный поиск решения, добавив новое ограничение D25 < 5.
Особенностью задач о назначениях является то, что переменные (значения изменяемых ячеек) являются булевыми переменными, т.е. могут принимать значение «0» либо «1».