Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
V. Матрицы и определители.
|
|
I. Решение систем линейных уравнений.
1. Решить систему линейных уравнений по правилу Крамера:
4х1 – 3х2 – 2х3 = 3,
2х1 – 4х2 – 3х3 = 0,
х1 + 2х2 + 3х3 = 5.
2. Исследовать и решить систему линейных уравнений:
х1 + 2х2 + 3х3 – 2х4 + х5 = 4,
3х1 + 6х2 + 5х3 – 4х4 + 3х5 = 5,
х1 + 2х2 + 7х3 – 4х4 + х5 = 11,
2х1 + 4х2 + 2х3 – 3х4 + 3х5 = 6.
3. Решить систему линейных уравнений сведением её к матричному виду:
х1 + 3х2 + 5х3 = -1,
х1 + х2 + 2х3 = 3,
2х1 + х2 + 3х3 = 0.
II. Понятие группы, кольца и поля.
4. Является ли группой множество чисел, кратных 3, относительно операции сложения?
5. Является ли кольцом множество чисел, кратных 7, относительно операций сложения и умножения?
6. Является ли группой множество квадратных невырожденных матриц n-порядка, определитель которых равен 1, относительно операции умножения?
7. Выясните, является ли полем кольцо всех матриц вида
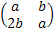 , где a, bÎ Q.
, где a, bÎ Q.
III. Свойства делимости целых чисел.
8. Доказать, что при любом натуральном n выражение n(n4 – 125n2 + 4) делится на 120.
9. Доказать, что если НОД(n, 6) = 1, то выражение n2 – 1 делится на 24.
10. Найти сумму остатков от деления числа 2008 на 2, 3, 4, 5, 11 и 25.
11. Доказать, что сумма трех последних натуральных степеней числа 5 делится на 155.
12. Доказать, что 5749 + 11155делится на 56.
13. Известно, что р и 8р2 + 1 – простые числа. Найти все такие числа р.
14. Найти наибольший общий делитель и наименьшее общее кратное чисел а, в и с двумя способами (с помощью алгоритма Евклида и с помощью разложения чисел на простые множители): а = 528, в = 154, с = 1816.
19. Найти натуральные числа а и в по следующим условиям:
ав = 8400, НОД(а, в) = 20.
20.Найти натуральные числа а и в по следующим условиям:
НОД(а, в) = 21, НОК(а, в) = 6006.
IV. Сравнения первой степени. Простейшие приемы решений сравнений первой степени и их систем.
15. Найти последнюю цифру числа 22008.
16. Решить сравнение: 84х º 12 (mod 30)
17. Решить систему уравнений:
4х º 7 (mod 13),
х º 2 (mod 17),
5х º 3 (mod 9),
8х º 4 (mod 14).
V. Матрицы и определители.
21.Решить уравнение: 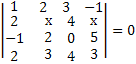
22. Решить матричное уравнение: