
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
XXII. Случайные процессы.
|
|
91. Задана случайная функция X(t) = U cos 3t, где U - случайная величина, причем M (U) = 1, D (U) = 1. Найти: а) математическое ожидание; б) корреляционную функцию; в) дисперсию случайной функции
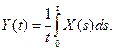
92. На выход дифференцирующего звена поступает случайная функция X(t), корреляционная функция которой Kx = [Dxcosw(t2 - t1)]/(t1 + t2). Найти корреляционную функцию выходной функции Y(t) = X’ (t).
93. Доказать, что при одновременной перестановке индексов и аргументов взаимная корреляционная функция двух случайных функций не изменяется: Rxy(t1, t2) = Ryx(t1, t2).
Математический анализ
I. Нахождение асимптот, исследование функций, построение графиков.
Пример 1. Найти асимптоты графика функции  .
.
Пример 2. Исследуйте функцию и постройте график  .
.
Пример 3. Исследуйте на монотонность и экстремумы функцию 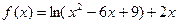 .
.