Пример. Построение модели регрессии с включением фак­тора времени.

Вернемся к данным табл. 10.1. Построим уравнение регрессии, описывающее зависимость расходов на конечное потребление y_t от совокупного дохода x_t и фактора времени. Для расчета параме­тров уравнения регрессии (10.8) воспользуемся обычным МНК. Система нормальных уравнений имеет вид:

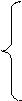Σ y_t = na+ b₁ Σ x_t+ b₂Σ t;

Σ y_tx_t= a Σ x_t + b₁ Σ x_t² + b₂ Σ t x_t; (10.9) Σ ty_t= a Σ t + b₁ Σ t x_t + b₂ Σ t;

Рассчитав по исходным данным необходимые величины, получим следующую систему:

86 = 8a+ 111b₁ + 36b₂;

1266= 111a + 1619b₁ + 554b₂; 440= 36a + 554b₁ + 204b₂;

Решив эту систему относительно а, b₁ и b₂, находим:

а = 1, 15; b₁ = 0, 49; b₂ ⁼ 0, 63.

Следовательно, построенное уравнение регрессии имеет вид:

y_t = 1, 15 + 0, 49 • х_t + 0, 63 • t

Интерпретация параметров этого уравнения следующая.

Параметр b₁ = 0, 49 характеризует, что при увеличении совокупное дохода на 1 д. е. расходы на конечное потребление возрастут в среднем на 0, 49 д. е. в условиях существования неизменной тен­денции. Параметр b ₂ = 0, 63 означает, что воздействие всех факторов, кроме совокупного дохода, на расходы на конечное потреб­ление приведет к его среднегодовому абсолютному приросту на 0, 63 д. е.

3-й учебный вопрос: Коинтеграция временных рядов – 30 мин.

Общий недостаток методов исключения тенденции заключа­ется в том, что эти методы предполагают некоторую модифика­цию исходной модели (10.1) вследствие либо замены переменных, либо до­бавления в эту модель фактора времени.

Однако большая часть соотношений, постулируемых экономической теорией, проверкой которых занималась эконометрика, была сформулирована в терминах уровней временных рядов, а не их последовательных разностей или отклонений от трендов, то есть предполагает измерение взаимосвязи переменных без включения в модель каких-либо до­полнительных факторов (например, переменной времени).

В некоторых случаях наличие в одном из временных рядов тенден­ции может быть следствием именно того факта, что другой ряд, включенный в модель, тоже содержит тенденцию, а не просто ре­зультатом прочих случайных причин.

Поэтому одинаковая или противоположная направленность тенденций рядов может иметь устойчивый характер и наблюдаться на протяжении длительного промежутка времени. При этом коэффициент корреляции, рассчитанный по уровням временных рядов, может соответственно не содер­жать ложной корреляции и характеризовать истинную причин­но-следственную зависимость между ними.

Начиная с 70-х гг. XX в., высказанные выше предположения были положены в основу новой теории коинтеграции времен­ных рядов.

Под коинтеграцией понимается причинно-следствен­ная зависимость в уровнях двух (или более) временных рядов, ко­торая выражается в совпадении или противоположной направ­ленности их тенденций и случайной колеблемости.

Не останавливаясь детально на положениях и концепциях те­ории коинтеграции (глубокое ее рассмотрение требовало бы под­готовки отдельного курса лекций), на данной лекции мы кратко охарактеризуем основные статистические методы и кри­терии, применяемые для проверки гипотез о наличии коинтегра­ции временных рядов данных.

В соответствии с теорией коинтеграции между двумя временными ря­дами существует коинтеграция в случае, если линейная комбина­ция этих временных рядов есть стационарный временной ряд (т. е. ряд, содержащий только случайную компоненту и имеющий постоянную дисперсию на длительном промежутке времени).

Рассмотрим уравнение регрессии вида (10.1). Остатки ε _t, в этом уравнении представляют собой линейную комбинацию рядов у_t и х_t:

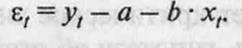(10.9)

Одним из методов тестирования гипотезы о коинтеграции временных рядов у_t и х_t является критерий Энгеля — Грангера.

Ал­горитм применения этого критерия следующий:

1. Выдвигается нуль-гипотеза об отсутствии коинтеграции между рядами у_t и х_t.

2. Рассчитывают параметры уравнения регрессии вида:

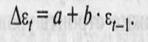(10.10)

где Δ ε _t, — первые разности остатков, полученных из соотношения (10.10).

3. Определяют фактическое значение t-критерия для коэф­фициента регрессии а в уравнении (10.10).

4. Сравнивают полученное значение с критическим значени­ем статистики t. Критические значения t, рассчитанные Энгелем и Грангером для уровня значимости 1%, 5% и 10%, составляют 2, 5899; 1, 9439; 1, 6177.

Если фактическое значение t больше кри­тического значения t для заданного уровня значимости а, нулевую гипотезу об отсутствии коинтеграции исследуемых временных рядов отклоняют и с вероятностью (1 – α) принимают альтерна­тивную гипотезу о том, что между рядами у_t и х_t есть коинтеграция. В противном случае гипотеза об отсутствии коинтеграции между исследуемыми рядами не отклоняется.

Другой метод тестирования нуль-гипотезы об отсутствии ко­интеграции между двумя временными рядами основан на ис­пользовании величины критерия Дарбина — Уотсона, получен­ной для уравнения (10.10).

Однако в отличие от традиционной ме­тодики его применения в данном случае проводят проверку гипо­тезы о том, что полученное фактическое значение критерия Дар­бина — Уотсона в генеральной совокупности равно нулю.

Ряд авторов называют следующие критические значения кри­терия Дарбина — Уотсона, полученные методом Монте-Карло для различных уровней значимости (α =0, 01; α =0, 05; α =0, 1):

для 1%-ного уровня — 0, 511;

для 5%-ного уровня — 0, 386;

для 10%-ного уровня — 0, 322.

Если результаты тестирования показали, что фактическое значение критерия Дарбина - Уотсона нельзя признать равным нулю (т. е. оно превышает критическое значение для заданного уровня значимости), нуль-гипотезу об отсутствии коинтеграции временных рядов отклоняют.

Если фактическое значение критерия Дарбина — Уотсона меньше критического значения для заданного уровня значи­мости, то нуль-гипотеза об отсутствии коинтеграции не откло­няется.

Коинтеграция двух временных рядов значительно упрощает процедуры и методы, используемые в целях их анализа, посколь­ку в этом случае можно строить уравнение регрессии и опреде­лять показатели корреляции, используя в качестве исходных дан­ных непосредственно уровни изучаемых рядов, учитывая тем са­мым информацию, содержащуюся в исходных данных, в полном объеме. Однако поскольку коинтеграция означает совпадение динамики временных рядов в течение длительного промежутка времени, то сама эта концепция применима только к временным рядам, охватывающим сравнительно длительные (например, в не­сколько десятилетий) промежутки времени.

При наличии корот­ких временных рядов данных, даже если формальные критерии показали наличие их коинтеграции, моделирование взаимосвязей по уровням этих рядов может привести к неверным результатам ввиду нарушения предпосылок теории коинтеграции.