Й учебный вопрос. Анализ мультиколлинеарности

Использование метода конфлюэнтного анализа во многих случаях оказалось недостаточно эффективным. Тогда специалисты по эконометрике стали использовать для отбора факторов, включаемых в уравнение регрессии, различные другие методы, среди которых наиболее распространенным стал анализ мультиколлинеарности.

Понятие «мультиколлинеарности» является одним из основополагающих понятий эконометрики.

Как уже отмечалось на первой лекции, явление линейной зависимости между двумя переменными называется коллинеарностью. Одновременная зависимость между несколькими переменными называется мультиколлинеарностью.

Считается, что нельзя одновременно включать в модель линейно зависимые (коллинеарные) переменные. Для оценки линейной зависимости между двумя переменными измеряют парные коэффициенты корреляции. Для проверки наличия мультиколлинеарности рассчитывают определитель матрицы коэффициентов парной корреляции. Считается, что если этот определитель близок к 0, то в системе факторных переменных присутствует мультиколлинеарность. Затем на основе анализа матрицы коэффициентов парной корреляции отбирают те переменные, которые принципиально можно включить в модель (уравнение регрессии).

Пусть x_i, x_j - разные факторные переменные, которые приобретают n различных значений.

Если r(х_i, х_j) > 0, 8, то факторы х₁ и х₂ считаются коллинеарными, и их нельзя одновременно включать в модель. Рекомендуется отбирать те факторы, для которых одновременно соблюдаются три условия:

1) r (x_i, x_j)< 0, 7, и одновременно при этом:

2) r (x_i, x_j)£ r (x_i, y)

3) r (x_i, x_j) £ r(x_j, y)

Таким образом, для выявления и анализа мультиколлинеарности используют следующие методы:

1. Анализируют матрицу парных коэффициентов корреляции между факторными (объясняющими) переменным. Считается, что если значения коэффициентов корреляции по абсолютной величине больше 0, 75 – 0, 80, то это свидетельствует о наличии мультиколлинеарности.

2. Если определитель матрицы оказывается близким к нулю, то это тоже свидетельствует о наличии мультиколлинеарности.

3. О наличии мультиколлинеарности говорят также некоторые внешние признаки, такие как:

- небольшое изменение исходных статистических данных приводит к существенному изменению оценок коэффициентов модели, вплоть до изменения знаков;

- оценки имеют большие стандартные ошибки, малую значимость, в то время, как модель в целом является значимой;

- оценки коэффициентов имеют неправильные с точки зрения экономической теории знаки или неоправданно большие значения.

Рассмотрим анализ мультиколлинеарности на том же примере.

Для расчета каждого коэффициента парной корреляции построим вспомогательную таблицу 2.6 (на примере расчета коэффициента корреляции между факторным признаком (показателем) x₁ и результативным показателем y). В этой таблице средние значения признаков находим по формулам:

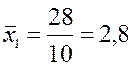
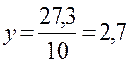
Таблица 2.6.

Вспомогательная таблица для расчета парного линейного коэффициента корреляции между показателями x₁ и y

Исходные данные	Вспомогательные расчеты
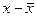
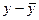
№/№	x1	y		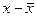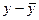	()2	()2	() ()
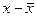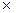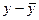			-1, 80	-1, 73	3, 24	2, 99	3, 11
			-0, 80	2, 27	0, 64	5, 15	-1, 82
			-0, 80	3, 27	0, 64	10, 69	-2, 62
		0, 8	-0, 80	-1, 93	0, 64	3, 72	1, 54
			0, 20	0, 27	0, 04	0, 07	0, 05
			0, 20	0, 27	0, 04	0, 07	0, 05
			0, 20	1, 27	0, 04	1, 61	0, 25
		0, 5	0, 20	-2, 23	0, 04	4, 97	-0, 45
		2, 5	1, 20	-0, 23	1, 44	0, 05	-0, 28
		1, 5	2, 20	-1, 23	4, 84	1, 51	-2, 71
Σ		27, 3		0, 00	11, 6	30, 86	-2, 84

 

 

После подсчета сумм в нижней строке таблицы, находим линейный коэффициент корреляции:

 

r (x₁ , y) =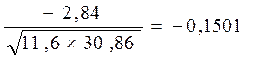

Делаем вывод о том, что связь между признаками слабая (так как по абсолютной величине коэффициент корреляции близок к 0) и обратная, так как коэффициент меньше 0. Отсюда следует, что такой фактор, как число членов семьи оказывает незначительное влияние на приобретение непродовольственных товаров. Поэтому, если требуется построить уравнение парной регрессии, включающее единственный факторный признак, не целесообразно в качестве этого признака выбирать фактор x₁.

Аналогично[1] рассчитываем коэффициенты парной корреляции между всеми остальными факторами и запишем их значения в виде матрицы (табл.2.7):

Таблица 2.7