Модель линейной парной регрессии.

2.1.1. Рассчитаем параметры a и b линейной регрессии у=а+bх.

Строим расчетную таблицу 1.

Таблица 1

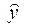
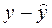
№	x	y	yx	x2	y2			Аi
	5, 3	18, 4	97, 52	28, 09	338, 56	16, 21	2, 19	11, 92
	15, 1	22, 0	332, 20	228, 01	484, 00	24, 74	-2, 74	12, 46
	24, 2	32, 3	781, 66	585, 64	1043, 29	32, 67	-0, 37	1, 14
	7, 1	16, 4	116, 44	50, 41	268, 96	17, 77	-1, 37	8, 38
	11, 0	22, 2	244, 20	121, 00	492, 84	21, 17	1, 03	4, 63
	8, 5	21, 7	184, 45	72, 25	470, 89	18, 99	2, 71	12, 47
	14, 5	23, 6	342, 20	210, 25	556, 96	24, 22	-0, 62	2, 62
	10, 2	18, 5	188, 70	104, 04	342, 25	20, 47	-1, 97	10, 67
	18, 6	26, 1	485, 46	345, 96	681, 21	27, 79	-1, 69	6, 48
	19, 7	30, 2	594, 94	388, 09	912, 04	28, 75	1, 45	4, 81
	21, 3	28, 6	609, 18	453, 69	817, 96	30, 14	-1, 54	5, 39
	22, 1	34, 0	751, 40	488, 41	1156, 00	30, 84	3, 16	9, 30
	4, 1	14, 2	58, 22	16, 81	201, 64	15, 16	-0, 96	6, 77
	12, 0	22, 1	265, 20	144, 00	488, 41	22, 04	0, 06	0, 26
	18, 3	28, 2	516, 06	334, 89	795, 24	27, 53	0, 67	2, 38
Σ	212, 0	358, 5	5567, 83	3571, 54	9050, 25	358, 50	0, 00	99, 69
среднее	14, 133	23, 900	371, 189	238, 103	603, 350	23, 90	0, 00	6, 65

Параметры a и b уравнения

Y_x = a + bx

определяются методом наименьших квадратов:

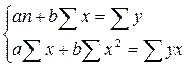
Разделив на n и решая методом Крамера, получаем формулу для определения b:

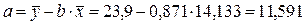
Уравнение регрессии:

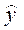=11, 591+0, 871x

С увеличением выпуска продукции на 1 тыс. руб. затраты на производство увеличиваются на 0, 871 млн. руб. в среднем, постоянные затраты равны 11, 591 млн. руб.

2.1.2. Тесноту связи оценим с помощью линейного коэффициента парной корреляции.

Предварительно определим средние квадратические отклонения признаков.

Средние квадратические отклонения:

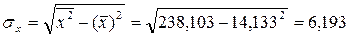
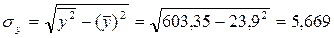
Коэффициент корреляции:

Между признаками X и Y наблюдается очень тесная линейная корреляционная связь.

2.1.3. Оценим качество построенной модели.

Определим коэффициент детерминации:

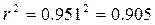
т. е. данная модель объясняет 90, 5% общей дисперсии у, на долю необъясненной дисперсии приходится 9, 5%.

Следовательно, качество модели высокое.

Найдем величину средней ошибки аппроксимации А _i.

Предварительно из уравнения регрессии определим теоретические значения 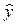для каждого значения фактора.

Ошибка аппроксимации А_i, i =1…15:

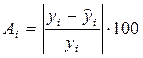
Средняя ошибка аппроксимации:

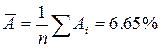
Ошибка небольшая, качество модели высокое.

4.1.4. Определим средний коэффициент эластичности:

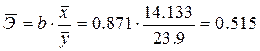
Он показывает, что с увеличением выпуска продукции на 1% затраты на производство увеличиваются в среднем на 0, 515%.

2.1.5. Оценим статистическую значимость полученного уравнения.
Проверим гипотезу H₀, что выявленная зависимость у от х носит случайный характер, т. е. полученное уравнение статистически незначимо. Примем α =0, 05. Найдем табличное (критическое) значение F- критерия Фишера:

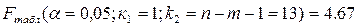
Найдем фактическое значение F - критерия Фишера:

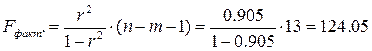
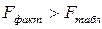
следовательно, гипотеза H₀ отвергается, принимается альтернативная гипотеза H₁: с вероятностью 1-α =0, 95 полученное уравнение статистически значимо, связь между переменными x и y неслучайна.

Построим полученное уравнение.