
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Учет инфляционных процессов в финансово-экономических расчетах.
|
|
Инфляция характеризуется обесцениванием национальной валюты (то есть снижением ее покупательной способности) и общим повышением цен в стране. Очевидно, что в различных случаях влияние инфляционного процесса сказывается неодинаково. Так, если кредитор (инвестор) теряет часть дохода за счет обесценивания денежных средств, то заемщик может получить возможность погасить задолженность деньгами со сниженной покупательной способностью.
Пусть Sα – сумма, покупательная способность которой с учетом инфляции равна покупательной способности суммы при отсутствии инфляции. Через ∆ S обозначим разницу между этими суммами.
Тогда отношение ∆ S/S, выраженное в процентах, называется уровнем инфляции.
При расчетах используют относительную величину уровня инфляции – темп инфляции α:
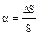
Тогда для определения Sα получаем следующее выражение:
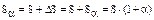 (1)
(1)
Величину (1 + α), показывающую, во сколько раз Sα больше S (то есть во сколько раз в среднем выросли цены), называют индексом инфляции – Iи:
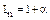 (2)
(2)
Динамика индекса инфляции за несколько лет отражает изменения, происходящие в инфляционных процессах. Понятно, что повышение индекса инфляции за определенный период по сравнению с предыдущим таким же периодом указывает на ускорение инфляции, снижение – уменьшение ее темпов.
Пусть α – годовой уровень инфляции. Это значит, что через год сумма Sα ' будет больше суммы S в (1+α) раз. По прошествии еще одного года сумма Sα '' будет больше суммы Sα ' в (1+α), то есть больше суммы S в (1+α)2 раз. Через n лет сумма Sα n вырастет по отношению к сумме S в (1+α)n раз. Отсюда видно, что инфляционный рост суммы S при годовом уровне инфляции α – то же самое, что и наращение суммы S по сложной годовой ставке процентов α.
Если известен годовой уровень инфляции α, то за период в n лет (при том, что n=na+nb и na – целое число лет, nb – оставшаяся нецелая часть года) индекс инфляции, очевидно, составит следующую величину:
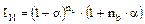 (3)
(3)
В некоторых случаях может быть задан уровень инфляции α m за короткий (меньше года) интервал. Тогда за период, составляющий m таких интервалов, индекс инфляции будет равен:
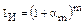 (4)
(4)
Если в обычном случае первоначальная сумма Р при заданной ставке процентов превращается за определенный период в сумму S, то в условиях инфляции она должна превратиться в сумму Sα, что требует уже иной процентной ставки.
Назовем ее ставкой процентов, учитывающей инфляцию.
Пусть
ia - ставка ссудного процента, учитывающая инфляцию;
da - учетная ставка, учитывающая инфляцию;
ja - номинальная ставка сложного процента, учитывающая инфляцию;
fa - номинальная сложная учетная ставка, учитывающая инфляцию.
Зададим годовой уровень инфляции a и простую годовую ставку ссудного процента i. Тогда для наращенной суммы S, превращающейся в условиях инфляции в сумму Sa, используем формулу (1.7):
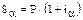
Для данной суммы можно записать еще одно соотношение:
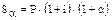 а затем составить уравнение эквивалентности:
а затем составить уравнение эквивалентности:
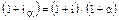 , из которого следует, что
, из которого следует, что
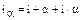 (5)
(5)
Мы получили, таким образом, известную формулу Фишера, в которой сумма (α + i× α) является величиной, которую необходимо прибавить к реальной ставке доходности для компенсации инфляционных потерь. Эта величина называется инфляционной премией.
Рассмотрим различные случаи начисления процентов с учетом инфляции. При этом всегда удобно пользоваться значением индекса инфляции. При этом всегда удобно пользоваться значением индекса инфляции за весь рассматриваемый период.
Для простых процентных ставок по формуле (1.7) получаем:
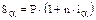
В то же время должно выполняться равенство:
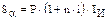
Составим уравнение эквивалентности:
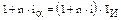 из которого получаем:
из которого получаем:
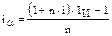 (6)
(6)
Для простых учетных ставок аналогичное уравнение эквивалентности будет иметь вид:
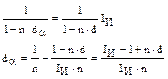
(7)
Для случая сложных процентов используем формулу:
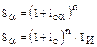 Отсюда
Отсюда
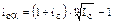 (8)
(8)
Если начисление процентов происходит несколько (m) раз в году, используем формулу:
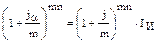 Отсюда
Отсюда
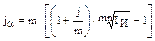 (9)
(9)
Таким образом, получаем две формулы для случая сложных учетных ставок:
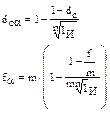
(10)
(11)
Используя полученные формулы, можно находить процентную ставку, компенсирующую потери от инфляции, когда заданы процентная ставка, обеспечивающая желаемую доходность фин. операции, и уровень инфляции в течение рассматриваемого периода. Эти формулы можно преобразовать и получить зависимость i от iα или любую другую. Например, из формулы (6) можно получить формулу, позволяющую определить реальную доходность фин. операции, когда задан уровень инфляции и простая ставка процентов, учитывающая инфляцию:
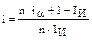 (12)
(12)
Из формулы (8) получаем аналогичную формулу для случая сложных процентов:
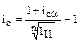 (13)
(13)
Подставив в последнюю формулу вместо индекса инфляции выражение (1+α)n, получим простую формулу:
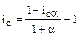 (14),
(14),
отражающую несколько очевидных соображений:
Если iсα = α (доходность вложений и уровень инфляции равны), то iс = 0, то есть весь доход поглощается инфляцией;
Если iсα < α (доходность вложений ниже уровня инфляции), то есть iс < 0, то есть операция приносит убыток;
Если iсα > α (доходность вложений выше уровня инфляции), то iс > 0, то есть происходит реальный прирост вложенного капитала.