
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Структурные средние. Средние структурные величины
|
|
Средние структурные величины.
При определении среднеструктурных величин определяются мода и медиана.
Величина средней определяется всеми значениями признака, встречающимися в данном ряду распределения. Различают такие структурные средние, как:
(1) мода
(2) медиана
(3) квартиль
(4) дециль
Медиана – вариант, расположенный в центре ранжированного ряда, медиана делит ряд на две одинаковые части, таким образом, чтобы по обе ее стороны находилось одинаковое число единиц совокупности. Если всем единицам ряда придать порядковые номера, то порядковый номер медианы будет определяться по формуле 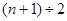 для рядов, где
для рядов, где 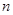 - нечетное, если же ряд с четным числом единиц, то медианой будет являться среднее значение между двумя вариантами, определенными по формуле:
- нечетное, если же ряд с четным числом единиц, то медианой будет являться среднее значение между двумя вариантами, определенными по формуле: 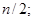
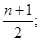
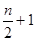 .
.
Нахождение медианы в интервальных вариационных рядах требует предварительного определения интервала, в котором находится медиана, т.е. медианного интервала – этот интервал характеризуется тем, что его коммулятивная частота равна полусумме или превышает полусумму всех частот ряда.
В зависимости от этого медиану определяют по формуле:
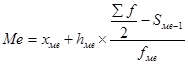
где 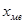 - нижняя граница медианного интервала;
- нижняя граница медианного интервала;
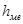 - ширина медианного интервала;
- ширина медианного интервала;
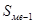 - сумма накопленных частот до частоты медианного интервала;
- сумма накопленных частот до частоты медианного интервала;
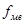 - частота медианного интервала.
- частота медианного интервала.
Пример.
Определить медиану, если:
| Стаж рабочих.лет | Численность раб. | Коммулята |
| 0-5 | ||
| 5-10 | ||
| 10-15 | ||
| 15-20 | ||
| 20 и более | ||
| Всего: |
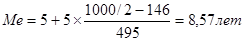
Вывод: из 1000 рабочих 500 чел. имеет стаж работы меньше 8, 57.лет.
Квартиль – это четвертая часть совокупности, определяется, как и медиана, только сумму частот необходимо разделить на 4, а при определении квартильного интервала коммулятивная частота должна быть больше или равна четверти суммы частот совокупности.
Мода – вариант, наиболее часто встречающийся в совокупности. В дискретном ряду мода – это вариант с наибольшей частотой. В интервальном вариационном ряду модой считают центральный вариант модального интервала. В пределах интервала надо определить то значение признака, который обладает наибольшей частотой. Определяем по формуле:
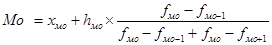
где 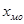 - нижний уровень модального интервала;
- нижний уровень модального интервала;
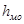 - ширина интервала;
- ширина интервала;
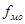 - частота интервала;
- частота интервала;
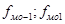 - частота предыдущего и последующего интервала.
- частота предыдущего и последующего интервала.
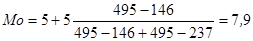
Дециль – делит совокупность на десять равных частей. Определяется аналогично, как и квартиль только сумму частот необходимо разделить на 10.
5. Средняя геометрическая.
Применяетсядля характеристики рядов динамики при определении средних темпов роста.
 , если
, если 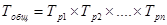 , тогда:
, тогда:
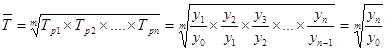 ;
;
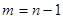 , т.е. число уровней ряда без одного или число темпов роста.,
, т.е. число уровней ряда без одного или число темпов роста.,
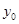 - начальный уровень ряда;
- начальный уровень ряда;
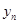 - конечный уровень ряда.
- конечный уровень ряда.
Пример. 
Определить цепные темпы роста и средний темп роста товарной продукции, если:
| Товарная Продукция млн. руб. |
 ;
; 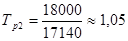 ;
; 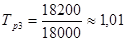 ;
;
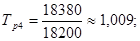
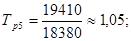
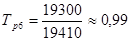
средний темп роста = 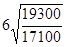 = 1, 0153
= 1, 0153
Лекция №7 Экономические индексы
1. Общие понятия об индексах.
Для характеристики явлений и процессов экономической жизни, статистика наряду с другими показателями использует индексы. Слово «индекс» в переводе – показатель.
Индекс – обобщающий показатель сравнения двух совокупностей, состоящих из элементов, которые непосредственно не подчиняются суммированию.
К совокупностям, элементы которых можно суммировать, относятся те совокупности, в которых дается сравнительная характеристика объемов: динамика посевных площадей, динамики выпуска конкретного вида продукции, динамики оплаты труда и т.д.
К совокупностям, элементы которых не поддаются суммированию, относятся такие 2 вида:
- характеристика 1 тонны пшеницы, молока, стали и т.д. В таких совокупностях рассчитывается индекс физического объема произведенной (проданной, потребленной) продукции;
- совокупности, где характеризуются цены (одной тонны пшеницы, молока и т.д.).
Для характеристики общего уровня цен (себестоимости, производительности, урожайности)применяются индексы себестоимости, цен и т.д.
Индексы применяются в следующих сферах:
1). Для сравнительной характеристики элементов конкретной совокупности;
2). Динамики;
3). Для пространственного сравнения;
4). Для сравнения факта с планом;
5). При факторном анализе.