
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Корреляционный и регрессионный анализ как метод изучения и прогнозирования экономических показателей
|
|
ЦЕЛЬ: Усвоить основные идеи корреляционного анализа и расчета коэффициента корреляции, овладеть методом построения регрессионных уравнений экономических показателей.
Процесс прогнозирования экономических показателей носит вероятностный характер, поэтому при прогнозировании их наибольший эффект дают методы корреляционного и регрессионного анализов.
Сначала проведем корреляционный анализ.
Предположим, что произведена выборка n значений показателя в ретроспективном периоде (или имеются данные n выборочных наблюдений) и влияющего на него фактора. В результате получен ряд значений признака (y)
y1, y2, …, yn
и влияющего на него фактора (x)
x1, x2, …, xn
Корреляционный анализ позволяет количественно оценить тесноту связи между признаком и фактором.
Наличие и количественную характеристику связи между признаком и фактором можно определить с помощью оценки коэффициента корреляции R, который вычисляется по формуле:
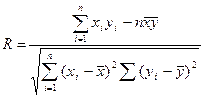 (1)
(1)
где средние значения х и у вычисляются по формулам:
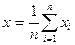 и
и 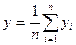
xi, yi - фактические значения фактора и признака при наблюдении или в год ретроспективного периода;
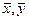 - среднее значение фактора и признака;
- среднее значение фактора и признака;
n - число наблюдений или число лет в ретроспективном периоде.
Коэффициент корреляции определяет тесноту связи между x и y и называется линейным коэффициентом корреляции.
Величина коэффициента корреляции изменяется
-1 _ R _ 1
При R = - 1 или R = 1 имеет место строгая пропорциональность в изменении y и x, при R =0 связь между y и x отсутствует, что обозначает их независимость.
Коэффициент корреляции вычисляется по выборочным данным и, как любой другой статистический показатель, может быть определен с некоторой погрешностью. При отсутствии корреляционной связи между признаками коэффициент корреляции в генеральной совокупности равен нулю, однако из-за случайного характера отбора данных выборочный коэффициент корреляции может быть и отличен от нуля. В связи с этим возникает необходимость проверки значимости коэффициента корреляции вычисленного на основании отбора данных. Выборочный коэффициент корреляции считается значимым, если выводы относительно наличия и характера корреляционной связи, сделанные на основании выборки, справедливы и для генеральной совокупности.
Рассмотрим способы оценки значимости коэффициента корреляции.
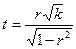
Каждому значению коэффициента корреляции соответствует случайная величина t, подчиненная распределению Стьюдента с К = n - 2 степенями свободы,

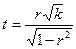
Вычисленное по этой формуле значение t сравнивают с критическим значением tk, a, которое находят по таблице распределения Стьюдента при заданных уровне значимости и числе степеней свободы К. Если 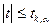 , то различие между выборочным коэффициентом корреляции и коэффициентом корреляции r, равным нулю, незначимо, а отличие от нуля r объясняется случайным характером отбора данных.
, то различие между выборочным коэффициентом корреляции и коэффициентом корреляции r, равным нулю, незначимо, а отличие от нуля r объясняется случайным характером отбора данных.
В практических расчетах уровень значимости a принимают равным 0, 05. Значения статистики Стьюдента при a = 0, 05 в зависимости от числа степеней свободы К приведены в таблице 1.
Таблица 1 – Распределение Стьюдента при a = 0, 05
| К | t | K | t | K | t | K | t | K | t |
| 12.71 | 2.26 | 2.12 | 2.06 | 2.01 | |||||
| 4.30 | 2.23 | 2.10 | 2.06 | 2.01 | |||||
| 3.18 | 2.20 | 2.09 | 2.05 | 2.00 | |||||
| 2.78 | 2.18 | 2.09 | 2.05 | 2.00 | |||||
| 2.57 | 2.16 | 2.08 | 2.05 | 1.99 | |||||
| 2.45 | 2.15 | 2.07 | 2.04 | 1.99 | |||||
| 2.37 | 2.13 | 2.07 | 2.03 | 1.98 | |||||
| 2.31 | 2.12 | 2.06 | 2.02 | 1.98 |
Затем производится регрессионный анализ. Он состоит из трех этапов:
1) логического анализа;
2) графического анализа;
3) определения уравнения теоретической линии регрессии, т.е. установления функциональной зависимости между признаком и фактором.
При логическом анализе эмпирических данных экономического показателя и значений влияющего на него фактора в ретроспективном периоде можно сделать некоторые предположения относительно наличия и направления связи между признаком и фактором.
На этапе графического анализа числовые значения фактора (xi) откладываются на оси абсцисс, а значение признака (yi)- на оси ординат. Точки на графике, соответствующие каждой паре значений xi и yi, образуют поле корреляции. По характеру расположения точек можно судить о направлении и форме связи. Соединив последовательно точки на плоскости, получим ломаную линию, называемую эмпирической линией регрессии. По ее виду можно предположить тип теоретической линии регрессии.
Экономико-математические модели прогноза строятся в виде уравнений регрессии, в которых в качестве зависимой переменной величины (функции) выступает экономический показатель, в качестве независимых переменных (аргументов) - формирующие его факторы.
Рассмотрим случай, когда экономический показатель зависит от одного фактора. Функция в таком случае называется однофакторной, а уравнение регрессии - парной регрессией.
Процесс нахождения теоретической линии регрессии заключается в выборе и обосновании типа кривой и расчете параметров ее уравнения. Теоретическая линия регрессии представляется в виде прямой либо плавной кривой, выражающейся математическим уравнением того или иного типа.
Наиболее распространенные математические формы связи результативного у и факторного х признаков следующие:
| Линейная | 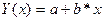
|
| Гиперболическая | 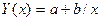
|
| Параболическая | 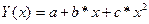
|
| Экспоненциальная | 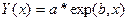
|
| Степенная | 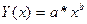
|
| Логарифмическая | 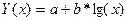
|
| Показательная | 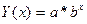
|
После выбора формы связи, рассчитываем параметры теоретического уравнения регрессии.
Способ расчета параметров теоретического уравнения регрессии основан на требовании максимальной близости ее к эмпирической линии регрессии. Для отыскания параметров используем метод наименьших квадратов, который основан на том, что из множества зависимостей вида у = f(x) наилучшим образом приближающейся к эмпирической линии регрессии является та, для которой сумма квадратов отклонений фактических значений признака от вычисленных по этому уравнению является наименьшей.
При линейной математической форме связи неизвестные коэффициенты и определяются из решения системы уравнений:
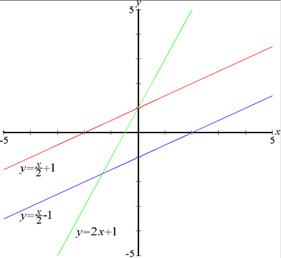
|
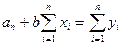 (2)
(2)
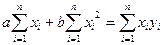
Решение этой системы:
 (3)
(3)
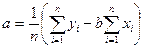
|
Для гиперболической зависимости система нормальных уравнений имеет вид:
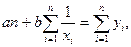 (4)
(4)
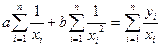
 Для параболической зависимости система из 3-х уравнений имеет вид:
Для параболической зависимости система из 3-х уравнений имеет вид:
|
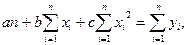
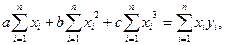 (5)
(5)
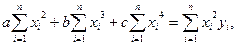
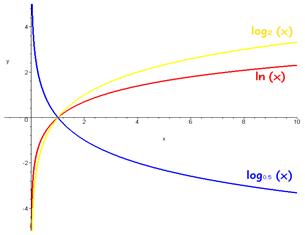
Для показательной регрессии параметры находятся из решения системы из 2-х уравнений:
|
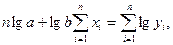 (6)
(6)
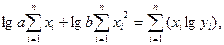
|
Для логарифмической регрессии решается система из следующих уравнений (7) для нахождения её параметров
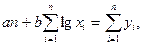 (7)
(7)
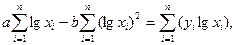
Системы (2), (4-7) можно решать способом алгебраического сложения, подстановки, методом Гаусса, Жордана - Гаусса, Крамера.
Если уравнение регрессии определяется в виде экспоненциальной или степенной зависимости, то путем замены и логарифмирования приводят ее к линейному виду и для линеаризованной функции используют систему нормальных уравнений вида (2)
Параметры экспоненциальной регрессии находят по формулам:
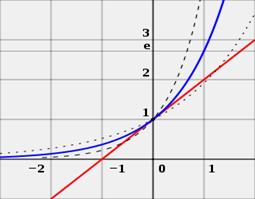
|

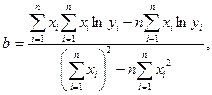 (8) y
(8) y
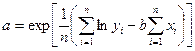
- степенной
|
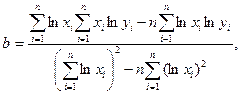 (9)
(9)
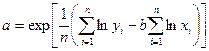
Оценку степени близости полученной экономико-математической модели к фактическим данным можно определить по корреляционному отношению:
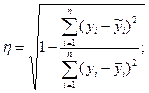
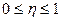 (10)
(10)
Ошибка уравнения регрессии, показывающая в среднем отклонения фактических данных от теоретических, равна:
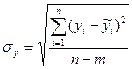 (11)
(11)
где n-m - число степеней свободы;
m - число определяемых в уравнении регрессии параметров.
Среднеквадратическое отклонение уравнения регрессии определяет меру близости эмпирических данных yi с ji теоретическими, найденным по уравнению регрессии.
Оценивается значимость уравнения регрессии. В связи с этим высказывается гипотеза, что все коэффициенты регрессии, кроме равны нулю (эта гипотеза называется нулевой и обозначается H0)/
Проверка гипотезы H0 осуществляется с помощью статистики Фишера:
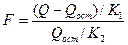
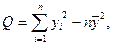 (12)
(12)
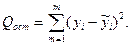
где Q, Qост - сумма квадратов отклонений результативного признака соответственно от среднего значения и от условного среднего 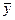 (х1, х2,..., хn); K1 = m; K2=n-m-1. При заданном уровне значимости a для степеней свободы К1 и К2 по таблице F - распределения
(х1, х2,..., хn); K1 = m; K2=n-m-1. При заданном уровне значимости a для степеней свободы К1 и К2 по таблице F - распределения
Фишера находят критическое значение F (К1, К2, a) и сравнивают его с расчетным, определенным по формуле (12). Если FVF (K!, K2, a) то гипотезу H0 об одновременном равенстве нулю всех коэффициентов регрессии отвергают и уравнение регрессии считают значимым. Если же F_F (K1, K2 a), то уравнение регрессии считают незначимым, т.е. отвергается влияние факторных признаков х1, х2,... хm на результативный. В практике статистических расчетов уровень значимости a принимают равным 0, 05. Это значит, что при F = F (К1, К2, a) вероятность того, что гипотеза Н0 справедлива, составляет 0, 05; при F> F (К1, К2, a) все коэффициенты регрессии могут иметь нулевые значения с вероятностью, меньшей 0, 05. Если же F< F (К1, К2, a), то вероятность справедливости нулевой гипотезы становится больше 0, 05 и ею уже нельзя пренебрегать. Значения F (К1, К2, a) при a= 0, 05 приведены в таблице 2.
Таблица 2 – Распределение Фишера при a = 0, 05
| К1¯ | ||||||||||
| К2 ¯ | ||||||||||
| 161.0 | 200.0 | 216.0 | 225.0 | 230.0 | 234.0 | 237.0 | 239.0 | 241.0 | 242.0 | |
| 18.51 | 19.0 | 19.16 | 19.25 | 19.30 | 19.33 | 19.36 | 19.37 | 19.38 | 19.39 | |
| 10.13 | 9.55 | 9.28 | 9.12 | 9.01 | 8.94 | 8.88 | 8.84 | 8.81 | 8.78 | |
| 7.71 | 6.94 | 6.59 | 6.39 | 6.26 | 6.16 | 6.09 | 6.04 | 6.00 | 5.96 | |
| 6.61 | 5.79 | 5.41 | 5.19 | 5.05 | 4.95 | 4.88 | 4.82 | 4.78 | 4.74 | |
| 5.99 | 5.14 | 4.76 | 4.53 | 4.39 | 4.28 | 4.21 | 4.15 | 4.10 | 4.06 | |
| 5.59 | 4.74 | 4.35 | 4.12 | 3.97 | 3.87 | 3.79 | 3.73 | 3.68 | 3.63 | |
| 5.32 | 4.46 | 4.07 | 3.84 | 3.69 | 3.58 | 3.50 | 3.44 | 3.39 | 3.34 | |
| 5.12 | 4.26 | 3.86 | 3.63 | 3.48 | 3.37 | 3.29 | 3.23 | 3.18 | 3.13 | |
| 4.96 | 4.10 | 3.71 | 3.48 | 3.33 | 3.22 | 3.14 | 3.07 | 3.02 | 2.97 | |
| 4.75 | 3.88 | 3.49 | 3.26 | 3.11 | 3.00 | 2.92 | 2.85 | 2.80 | 2.76 | |
| 4.60 | 3.74 | 3.34 | 3.11 | 2.96 | 2.85 | 2.77 | 2.70 | 2.65 | 2.60 | |
| 4.49 | 3.63 | 3.24 | 3.01 | 2.85 | 2.74 | 2.66 | 2.59 | 2.54 | 2.49 | |
| 4.41 | 3.55 | 3.16 | 2.93 | 2.77 | 2.66 | 2.58 | 2.51 | 2.46 | 2.41 | |
| 4.35 | 3.49 | 3.10 | 2.87 | 2.71 | 2.60 | 2.52 | 2.45 | 2.40 | 2.35 | |
| 4.24 | 3.38 | 2.99 | 2.76 | 2.60 | 2.49 | 2.41 | 2.34 | 2.28 | 2.24 | |
| 4.17 | 3.32 | 2.92 | 2.69 | 2.53 | 2.42 | 2.34 | 2.27 | 2.21 | 2.16 | |
| 4.08 | 3.23 | 2.84 | 2.61 | 2.45 | 2.34 | 2.25 | 2.18 | 2.12 | 2.07 | |
| 4.03 | 3.18 | 2.79 | 2.56 | 2.40 | 2.29 | 2.20 | 2.13 | 2.07 | 2.02 | |
| 4.00 | 3.15 | 2.76 | 2.52 | 2.37 | 2.25 | 2.17 | 2.10 | 2.04 | 1.99 | |
| 3.96 | 3.11 | 2.72 | 2.48 | 2.33 | 2.21 | 2.12 | 2.05 | 1.99 | 1.95 | |
| 3.94 | 3.09 | 2.70 | 2.46 | 2.30 | 2.19 | 2.10 | 2.03 | 1.87 | 1.92 |
Уравнение регрессии позволяет установить характер влияния факторных признаков на результативный.
По знаку коэффициента регрессии определяется направление влияния признака на результативный признак: положительный знак указывает на возрастание исследуемой величины при увеличении фактора отрицательный - на ее уменьшение.
Абсолютное значение коэффициента регрессии показывает, насколько единиц увеличится (уменьшится) результативный признак при увеличении факторного на единицу.
С помощью полученного уравнения регрессии можно определить выровненные значения показателя в ретроспективном периоде, подставив фактические значения x в уравнение регрессии. Прогноз показателя осуществляется следующим образом: в найденную функцию подставляют задаваемые значения фактора в прогнозируемом периоде и получают планируемую величину показателя.
Если имеется динамический ряд изменения экономического показателя, то процесс прогнозирования можно изобразить, как показано на рис.1.
Пусть уравнение связи y = f(t)
 |  | ||||
 | |||||
Y Аппроксимация Экстраполяция
 |

0 1 2 n n+1 n+k t
Рис. 1. Процесс прогнозирования
 эмпирическая линия регресии;
эмпирическая линия регресии;
 теоретическая линия регресии;
теоретическая линия регресии;
k - длина планируемого периода.