Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Контрольный пример
|
|
Задание: Построить экономико-математическую модель платежеспособного спроса на продукты питания от уровня доходов семьи по данным проведенного опроса 8 групп семей (в т.грн). Спрогнозировать уровень расходов на питание при доходе 20.2, 22.4 и 26.5 тыс.грн
Таблица 1 – Исходные данные
| Доходы семьи (х) | 1, 4 | 3, 3 | 5, 5 | 7, 6 | 9, 8 | 12, 0 | 14, 7 | 18, 9 |
| Расходы на питание (у) | 1, 1 | 1, 4 | 2, 0 | 2, 4 | 2, 8 | 3, 1 | 3, 5 | 4, 0 |
Построим график зависимости
Рисунок 1 – График зависимости расходов на питание от доходов семьи
Исходя из построенного графика, можно предположить наличие прямой линейной зависимости. Проверим данное предположение, рассчитав линейный коэффициент корреляции Пирсона. Составим вспомогательную таблицу.
Таблица 2 – Дополнительные расчеты
| N | Доходы семьи (Хi) | Расходы на питание (Yi) | Xi*Yi | (Xi-Xcp)^2 | (Yi-Ycp)^2 | Хi^2 |
| 1, 4 | 1, 1 | 1, 54 | 60, 06 | 2, 07 | 1, 96 | |
| 3, 3 | 1, 4 | 4, 62 | 34, 22 | 1, 29 | 10, 89 | |
| 5, 5 | 13, 32 | 0, 29 | 30, 25 | |||
| 7, 6 | 2, 4 | 18, 24 | 2, 40 | 0, 02 | 57, 76 | |
| 9, 8 | 2, 8 | 27, 44 | 0, 42 | 0, 07 | 96, 04 | |
| 3, 1 | 37, 2 | 8, 12 | 0, 32 | |||
| 14, 7 | 3, 5 | 51, 45 | 30, 80 | 0, 93 | 216, 09 | |
| 18, 9 | 75, 6 | 95, 06 | 2, 14 | 357, 21 | ||
| Итого | 73, 2 | 20, 3 | 227, 09 | 244, 42 | 7, 12 | 914, 2 |
| Среднее | 9, 15 | 2, 5375 | х | х | х | х |
Оценим корреляционную связь между фактором и признаком по формуле (1)
R = 0, 99118051
Коэффициент корреляции указывает на весьма тесную прямую связь между доходами и расходами семьи на продукты питания.
Проверим значимость коэффициента корреляции с помощью критерия Стьюдента t=25.853. Т.к. полученное t (25.853) больше tk, a (2.45), то R значим.
Определим параметры линейного уравнения регрессии вида y=a+b*x из системы уравнений (2):
8a + 73, 2b = 20, 3
73, 2a + 914, 2b = 227, 09
По формулам (3): b = 0, 169156 и a=0, 989727
Экономико-математическая модель расходов на продукты питания в зависимости от уровня дохода семей имеет вид:
X
С экономической точки зрения полученное уравнение означает: минимальные расходы семьи на питание (даже если доходов в периоде не было) составляют 0, 99 тыс.грн. При росте доходов семьи на 1 тыс.грн расходы на питание возрастут на 0, 17 тыс.грн.
Проверим точность расчётов и определим: является ли полученное уравнение регрессии наиболее близким к эмпирической линии регрессии и самым точным?
Для этого воспользуемся предложенными программами и предложенными формулами (10) и (11), а результаты занесем в 2 таблицы.
Таблица 3 – Сводная таблица основных результатов
| Показатель | Программа | Результат |
| Коэффициент корреляции | KOR. EXE | 0, 99118 |
| Уравнение линейной регрессии | LIN. EXE | y= 0, 9897+0, 1692*x |
| Уравнение параболической регрессии | PARAB. EXE | y= 0, 716 + 0, 249*x - 0, 004*x^2 |
| Уравнение гиперболической регрессии | GIPER. EXE | y= 3, 297 - 3, 714/x |
| Уравнение степенной регрессии | STEP. EXE | y= 0, 845*x^0, 52 |
| Уравнение показательной регрессии | POKAZ. EXE | y= 1, 20*1, 075^x |
| Уравнение экспоненциальной регрессии | EXP. EXE | y= 1, 203*exp(0, 073*x) |
| Уравнение логарифмической регрессии | LOGAR. EXE | y= 0, 32 + 1, 133*LOG(x) |
Таблица 4 – Вспомогательные расчеты для определения наиболее близкого уравнения регрессии
| N | Õ i | Yi | Y lin | (Yi-Ylin)^2 | Y parab | (Yi-Ypar)^2 | Y giper | (Yi-Ygip)^2 | Y step | (Yi-Yst)^2 | Y pokaz | (Yi-Ypo)^2 | Y exp | (Yi-Yex)^2 | Y logar | (Yi-Ylog)^2 |
| 1, 4 | 1, 1 | 1, 23 | 0, 017 | 1, 06 | 0, 002 | 0, 64 | 0, 212 | 1, 01 | 0, 008 | 1, 33 | 0, 053 | 1, 33 | 0, 053 | 0, 7 | 0, 160 | |
| 3, 3 | 1, 4 | 1, 55 | 0, 023 | 1, 49 | 0, 008 | 2, 17 | 0, 593 | 1, 57 | 0, 029 | 1, 53 | 0, 017 | 1, 53 | 0, 017 | 1, 67 | 0, 073 | |
| 5, 5 | 1, 92 | 0, 006 | 1, 97 | 0, 001 | 2, 62 | 0, 384 | 2, 05 | 0, 002 | 1, 79 | 0, 044 | 1, 79 | 0, 044 | 2, 25 | 0, 063 | ||
| 7, 6 | 2, 4 | 2, 28 | 0, 014 | 2, 38 | 0, 000 | 2, 81 | 0, 168 | 2, 43 | 0, 001 | 2, 09 | 0, 096 | 2, 09 | 0, 096 | 2, 62 | 0, 048 | |
| 9, 8 | 2, 8 | 2, 65 | 0, 023 | 2, 77 | 0, 001 | 2, 92 | 0, 014 | 2, 77 | 0, 001 | 2, 45 | 0, 123 | 2, 45 | 0, 123 | 2, 91 | 0, 012 | |
| 3, 1 | 3, 02 | 0, 006 | 3, 13 | 0, 001 | 2, 99 | 0, 012 | 3, 08 | 0, 000 | 2, 88 | 0, 048 | 2, 88 | 0, 048 | 3, 14 | 0, 002 | ||
| 14, 7 | 3, 5 | 3, 48 | 0, 000 | 3, 51 | 0, 000 | 3, 04 | 0, 212 | 3, 42 | 0, 006 | 3, 5 | 0, 000 | 3, 5 | 0, 000 | 3, 37 | 0, 017 | |
| 18, 9 | 4, 19 | 0, 036 | 3, 99 | 0, 000 | 3, 1 | 0, 810 | 3, 9 | 0, 010 | 4, 75 | 0, 563 | 4, 75 | 0, 563 | 3, 65 | 0, 123 | ||
| прогноз1 | 20, 2 | ? | 4, 41 | x | 4, 11 | x | 3, 11 | x | 4, 04 | x | 5, 22 | x | 5, 22 | x | 3, 73 | x |
| ï ð î ã í î ç 2 | 22, 4 | ? | 4, 78 | x | 4, 28 | x | 3, 13 | x | 4, 26 | x | 6, 13 | x | 6, 13 | x | 3, 84 | x |
| прогноз3 | 26, 5 | ? | 5, 47 | x | 4, 5 | x | 3, 16 | x | 4, 65 | x | 8, 26 | x | 8, 26 | x | 4, 03 | x |
| S | 0, 126 | 0, 013 | 2, 405 | 0, 058 | 0, 943 | 0, 943 | 0, 497 | |||||||||
| s | 0, 145 | 0, 051 | 0, 633 | 0, 098 | 0, 397 | 0, 397 | 0, 288 | |||||||||
| h | 0, 991 | 0, 999 | 0, 814 | 0, 996 | 0, 931 | 0, 931 | 0, 964 |
Таким образом, наименьшая ошибка параболического уравнения регрессии (0, 051) при максимальном значении h, значит для прогнозирования данных (апроксимации или экстраполяции) будет использовано уравнение вида : y= 0, 716 + 0, 249*x - 0, 004*x^2.
Нанесем на график эмпирическую линию и три наиболее близких линии регрессии (линейная, параболическая, степенная).
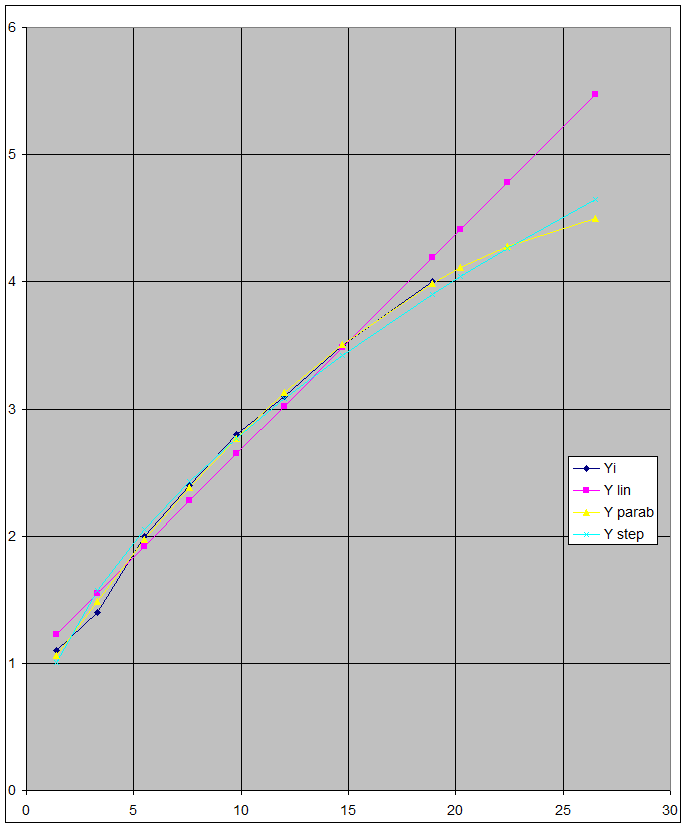Рисунок 2 – Линии регрессии и прогнозирование данных
Ошибка параболического уравнения регрессии находится в допустимых пределах, но можно окончательно убедиться в значимости параметров уравнения регрессии с помощью статистики Фишера (12) и проверки гипотезы Но.
Q = 7.11875 Qост=0, 013 F = 728.7949
Сравним полученное значение F с табличным F (К1, К2, a): 728.7949> 6.59. Значит, гипотеза Но отвергается и параметры уравнения считаются значимыми.
Выводы:
1. Зависимость между расходами на питание и доходами семьи носит прямой характер, а тесноту связи можно охарактеризовать как очень тесную, переходящую в функциональную (R=0.99).
2. Поскольку R значим и указывает на тесную связь между признаками, можно провести регрессионный анализ зависимости.
3. Выбрано самое близкое из рассчитанных уравнений регрессии – параболическое вида y= 0, 716 + 0, 249*x - 0, 004*x^2. Ошибка уравнения регрессии не существенная и параметры уравнения значимы.
4. Для заданных уровней доходов семей определены прогнозные значения расходов:
при доходах в размере 20.2 тыс.грн расходы на питание составят 4.11 тыс.грн
при доходах 22.4 тыс грн расходы на питание достигнут величины 4.28 тыс.грн
при доходах 26.5 тыс.грн можно ожидать расходы на питание в размере 4.5 тыс.грн
5. В общем виде полученное уравнение регрессии можно так экономически интерпретировать: поскольку ветки параболы опущены вниз, то максимальное значение У (расходы на питание) будет достигнуто в её вершине при доходах (Х) равных 31.125 тыс.грн. При этом расходы составят 4.585 тыс.грн. Если вспомнить поведение параболы при достижении её вершины и учесть угол наклона ветвей параболы, то можно сделать вывод, что при доходах семьи от 25 до 37 тыс.грн расходы будут различаться незначительно и составлять в среднем 4.5 тыс.грн.