Ревізія законів Кеплера

Отже, Кеплер відкрив свої закони емпіричним шляхом. Нью­тон же вивів закони Кеплера із закону всесвітнього тяжіння. У результаті цього зазнали змін перший і третій закони. Перший закон Кеплера був узагальнений, і його сучасне формулювання звучить так: траєкторії руху небесних тіл у центральному полі тяжіння являють собою конічні перерізи (криву II порядку) — еліпс, коло, параболу або гіперболу, в одному з фокусів якої міститься центр мас системи.

Форма траєкторії визначається величиною повної енергії рухомого тіла, що у гравітаційному полі складається з кінетичної енергії К рухомого тіла масою от, швидкістю v і потенціальної енергії U тіла, що перебуває в гравітаційному полі на відстані г від тіла з масою М. При цьому діє закон збереження повної енергії тіла:

E = K+U = const; ,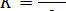

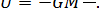
Закон збереження енергії можна переписати у вигляді:

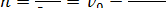
Константа h називається сталою енергії. Вона прямо пропорційна повній механічній енергії тіла Е і залежить тільки від початкового радіус-вектора і початкової швидкості u₀. За h< 0 кінетичної енергії тіла недостатньо для подолання гравітаційного зв’язку. Величина радіус-вектора тіла обмежена зверху, тож відбувається обертання по замкнутій, еліптичній орбіті. Такий рух можна уподібнити руху маятника той самий перехід кінетичної енергії в потенціальну під час підйому і зворотний під час опускання. Подібний рух називається фінітним, тобто замкнутим. Для h = 0 за необмеженого зростання радіус-вектора тіла його швидкість зменшується до нуля це рух по параболі. Такий рух інфінітний, необмежений у просторі. За h> 0 кінетична енергія тіла досить велика і на нескінченній відстані від притягувального центра тіло матиме ненульову швидкість віддалення від нього це рух по гіперболі. Таким чином, можна сказати, що тіло рухається відносно притягувального центра тільки по орбітах, що є конічними перерізами. Як випливає з формули (2), наближення тіла до притягувального центра завжди має супроводжуватися збільшенням орбітальної швидкості тіла, а віддалення зменшенням згіднoз другим законом Кеплера. Другий закон Кеплера не піддавався ревізії, а от третій було уточнено.

В узагальненому вигляді цей закон зазвичай формулюється (4) так: добуток сум мас небесних тіл і їхніх супутників із квадратами їхніх сидеричних періодів обертання відносяться як куби великих півосей їхніх орбіт:

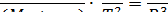
де М₁ і М₂ — маси небесних тіл, m₁ і т₂ — відповідно маси їхніх супутників R₁ і R₂великі півосі їхніх орбіт, Т₁ і Т₂ — сидеричні періоди обертання. Необхідно зрозуміти, що закон Кеплера пов’язує характеристики руху компонентів будь-яких довільних і незалежних космічних систем. У цю формулу можуть входити одночасно Марс із супутником, і Земля з Місяцем, чи Сонце з Юпітером.