
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Исследование центральных характеристик выборки. Построение графиков распределения
|
|
Для проверки эффективности новой развивающей программы были созданы две группы детей шестилетнего возраста. На первом этапе дети обеих групп были протестированы по методике Керна-Иерасика (школьная зрелость). Результаты тестирования по невербальной шкале занесены в таблицу (Х – контрольная группа, Y – экспериментальная группа). Сделать сравнительный анализ школьной зрелости детей этих групп.
Цель задания. Построить таблиц распределения частот и графиков распределения частот. Выявление центральных тенденций распределения. Освоить методы расчета моды, медианы, среднего арифметического, дисперсии и стандартного отклонения системы упорядоченных событий. Рассчитать параметры отклонения распределения от нормального.
Таблица 1 - Результаты тестирования по невербальной шкале
по методике Керна-Иерасика (школьная зрелость)
(сырые баллы: X – контрольная группа, Y – экспериментальная группа)
| X | Y |
Решение. Для решения задачи перенесём данные из таблицы в условии задания на лист рабочей книги MS Excel.
1) Найдём максимальное, минимальное значение и размах для выборки X:
Max = 77
Min = 45
L = Max – Min = 32
2) Разобьём отрезок [Min; Max] на 5 равных по длине интервалов (см. табл. 2).
Таблица 2 – Результаты вычислений
абсолютной, относительной и накопительной частот
(контрольная группа)
| Интервалы [a; b] | Частота | |||
| A | b | Абсолютная | Относительная | Накопленная |
| 42, 3 | 47, 7 | 0, 1 | 0, 1 | |
| 58, 3 | 0, 1 | 0, 2 | ||
| 58, 3 | 63, 7 | 0, 2 | 0, 4 | |
| 63, 7 | 0, 1 | 0, 5 | ||
| 74, 3 | 0, 2 | 0, 7 | ||
| 74, 3 | 79, 7 | 0, 3 | 1, 00 | |
| 79, 7 | 0, 00 | 1, 00 | ||
| Шаг = 5, 3 |
Используя данные таблицы 2, построим гистограмму абсолютных частот для контрольной группы X (рис. 1).
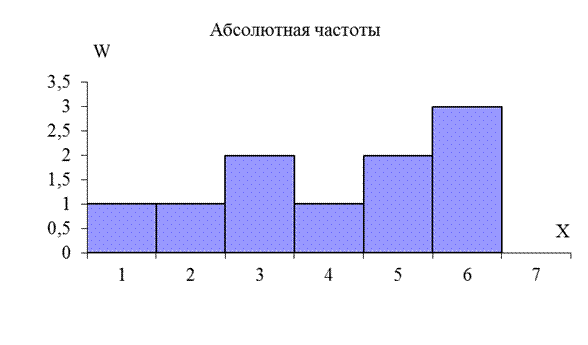
Рисунок 1 – Гистограмма абсолютных частот (контрольная группа)
Используя данные таблицы 2, построим гистограмму относительных частот для контрольной группы X (рис. 2).
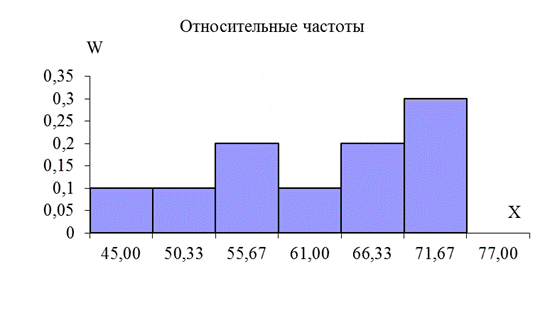
Рисунок 2 – Гистограмма относительных частот (контрольная группа)
Используя данные таблицы 2, построим гистограмму накопленных частот для контрольной группы X (рис. 3).
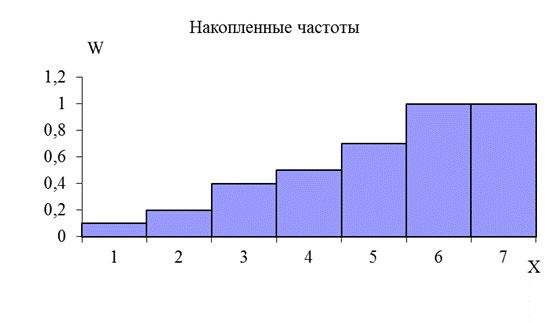
Рисунок 3 – Гистограмма накопленных частот (контрольная группа)
Таблица 3 – Результаты вычислений
абсолютной, относительной и накопительной частот
(экспериментальная группа)
| Интервалы [a; b] | Частота | |||
| A | b | Абсолютная | Относительная | Накопленная |
| 87, 3 | 92, 7 | 0, 1 | 0, 1 | |
| 98, 0 | 103, 3 | 0, 4 | 0, 5 | |
| 103, 3 | 108, 7 | 0, 2 | 0, 7 | |
| 108, 7 | 114, 0 | 0, 1 | 0, 8 | |
| 114, 0 | 119, 3 | 0, 1 | 0, 9 | |
| 119, 3 | 124, 7 | 0, 1 | 1, 00 | |
| 124, 7 | 130, 0 | 0, 00 | 1, 00 | |
| Шаг = 5, 3 |
Используя данные таблицы 3, построим гистограмму относительных частот для контрольной группы Y (рис. 4).
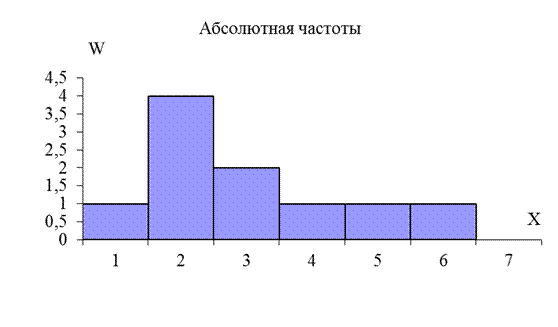
Рисунок 4 – Гистограмма абсолютных частот (экспериментальная группа)
Используя данные таблицы 3, построим гистограмму относительных частот для контрольной группы Y (рис. 5).
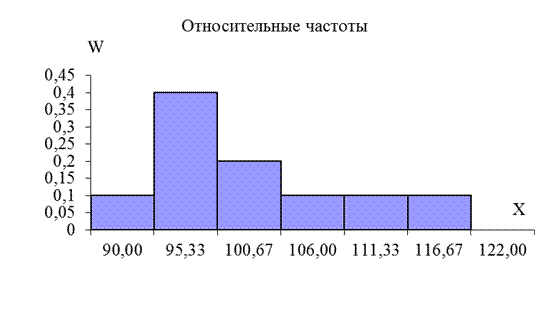
Рисунок 5 – Гистограмма относительных частот (экспериментальная группа)
Используя данные таблицы 3, построим гистограмму накопленных частот для экспериментальной группы Y (рис. 6).
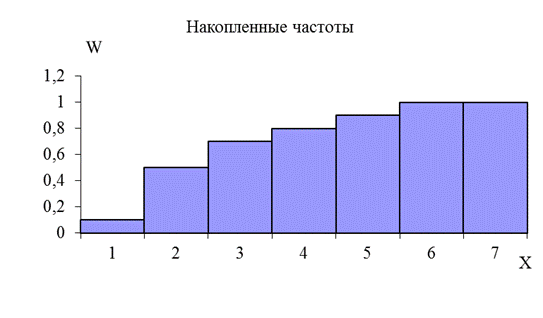
Рисунок 6 – Гистограмма накопленных частот (экспериментальная группа)
Теперь определим следующие выборочные характеристики.
Мода – это такое значение из множества измерений, которое встречается наиболее часто. Моде, или модальному интервалу признака, соответствует наибольший подъём (вершина) графика распределения частот. Если график распределения частот имеет одну вершину, то такое распределение называется унимодальным.
Медиана – это такое значение признака, которое делит упорядоченное (ранжированное) множество данных пополам так, что одна половина всех значений оказывается меньше медианы, а другая больше. Таким образом, первым шагом при определении медианы является упорядочивание (ранжирование) всех значений по возрастанию или убыванию. Далее медиана определяется следующим образом:
- если данные содержат не чётное число значений, то медиана есть центральное значение;
- если данные содержат чётное число значений, то медиана есть точка, лежащая посередине между двумя центральными значениями.
Размах выборки определяется по формуле: L =  .
.
Среднее (выборочное среднее, среднее арифметическое) – определяется как сумма всех значений измеренного признака, делёная на количество суммированных значений.
 ,
,
где 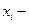 измеренная величина,
измеренная величина, 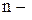 количество измеренных значений.
количество измеренных значений.
Выборочное среднее характеризует среднее значение экспериментального показателя в выборке наблюдений.
Выборочная дисперсия характеризует меру рассеяния случайной величины относительно математического ожидания (выборочного среднего значения) и вычисляются по формуле:
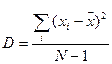
Стандартное отклонение (сигма, среднеквадратическое отклонение) – положительное значение квадратного корня из дисперсии:
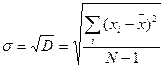
Асимметрия – мера симетричности графика частот – вычисляются по формуле:
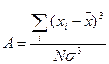
Если 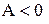 , то эмпирическое распределение несимметрично и сдвинуто вправо. При
, то эмпирическое распределение несимметрично и сдвинуто вправо. При 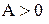 распределение имеет сдвиг влево. При
распределение имеет сдвиг влево. При 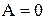 распределение симметрично.
распределение симметрично.
Эксцесс Е - мера плосковершинности или остроконечности графика распределения изменённого признака вычисляется по формуле:
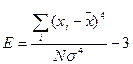
Островершинное распределение характеризуется положительным эксцессом (E> 0), а плосковершинное – отрицательным (-3< E< 0). «Средневершинное» (нормальное) распределение имеет нулевой эксцесс (E = 0).
Используя специальные функции MS Excel вычислим выборочные характеристики для X и Y. Результаты вычислений оформлены в виде таблицы 3.
Таблица 3 – Результаты вычислений выборочных характеристик
| Характеристика | X | Y |
| Счет | ||
| Сумма | ||
| Мода | Нет | нет |
| Выборочное среднее | 66, 50 | 104, 00 |
| Дисперсия | 109, 17 | 107, 56 |
| Медиана | 70, 00 | 103, 50 |
| Асимметрия | -0, 96 | 0, 36 |
| Эксцесс | 0, 29 | -0, 80 |
| Минимальное значение | 45, 00 | 90, 00 |
| Максимальное значение | 665, 00 | 1040, 00 |
| Размаха | 620, 00 | 950, 00 |
| Стандартное отклонение | 10, 45 | 10, 37 |
Для вычисления были использованы следующие функции MS Excel:
- функция СРЗНАЧ вычисляет среднее арифметическое из нескольких массивов (аргументов) чисел
- функция МЕДИАНА позволяет получать медиану заданной выборки
- функция МОДА вычисляет наиболее часто встречающееся значение в выборке
- функция ДИСП позволяет оценить дисперсию по выборочным данным
- функция СТАНДОТКЛОН вычисляет стандартное отклонение
- функция ЭКСЦЕСС вычисляет оценку эксцесса по выборочным данным
- функция СКОС позволяет оценить асимметрию выборочного распределения.
Таким образом, при выполнении задания были простроены таблицы распределения частот и графики распределения частот, определены центральные тенденции распределения: расчета моды, медианы, среднего арифметического, меры рассеяния: выборочная дисперсия и стандартное отклонение, а также параметры отклонения распределения от нормального: асимметрия и эксцесс. Графики распределения частот и значения выборочных характеристик позволяют выдвинуть гипотезу о существенности отличий школьной зрелости у детей (протестированных по методике Керна-Иерасика) в группах Х (контрольная группа) и Y (экспериментальная группа).