
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Расчет корреляционной связи между двумя признаками
|
|
У участников психологического эксперимента был измерен уровень соперничества (по тесту Томаса) и стиль общения (по тесту Журавлева). Полученные данные занесены в таблицу 6. Можно ли утверждать, что люди, склонные к соперничеству, предпочитают деспотичный стиль общения? Можно ли утверждать, что люди, склонные к соперничеству, предпочитают коллегиальный или либеральный стиль общения?
Цель задания. Освоить метод корреляционного анализа и построить график двумерного рассеяния.
Таблица 6 – Результаты психологического исследования уровня
соперничества (по тесту Тамаса) и стиля общения (по тесту Журавлева)
| № респон-дента | Возраст | Уровень соперничества | Деспотический стиль общения | Коллегиальный стиль общения | Либеральный стиль общения | |
Решение. Для решения задачи перенесём данные из таблицы 6 в лист рабочей книги MS Excel.
Построим графики двумерного рассеяния случайной величины (X, Y), где X – уровень соперничества, Y – стиль общения: деспотический (рис.8), коллегиальный (рис.9), и либеральный (рис.10).
Для оценки степени взаимосвязи величин X и Y, измеренных в количественных шкалах, используется коэффициент линейной корреляции (коэффициент Пирсона), предполагающий, что выборки X и Y распределены по нормальному закону.
Коэффициент корреляции – параметр, который характеризует степень линейной взаимосвязи между двумя выборками, рассчитывается по формуле:
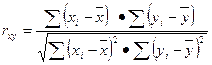
Коэффициент корреляции изменяется от -1 (строгая обратная линейная зависимость) до 1 (строгая прямая линейная зависимость). При значении 0 линейной зависимости между двумя выборками нет.
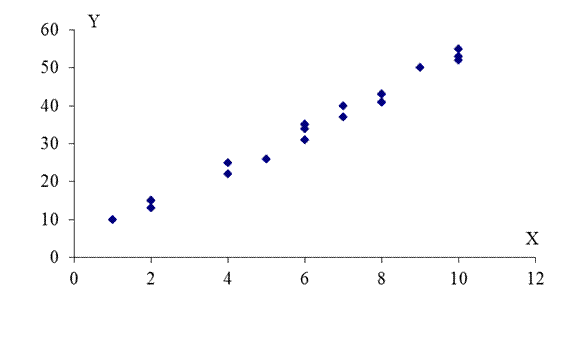
Рисунок 8 – График двумерного рассеяния
(X – уровень соперничества, Y – деспотический стиль общения)
В MS Excel для вычисления парных коэффициентов линейной корреляции Пирсона можно пользоваться статистической функцией КОРРЕЛ (массив1; массив2), где массив1 – ссылка на диапазон ячеек первой выборки (X); массив2 – ссылка на диапазон ячеек второй выборки (Y).
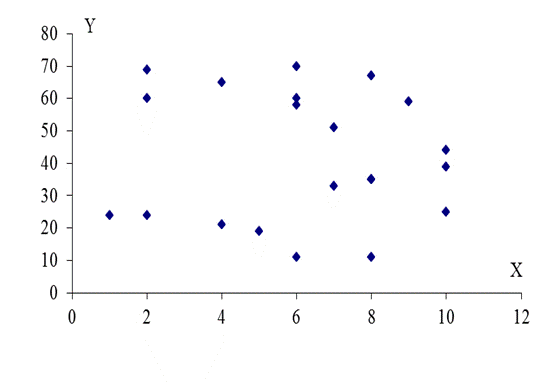
Рисунок 9 – График двумерного рассеяния
(X – уровень соперничества, Y – коллегиальный стиль общения)
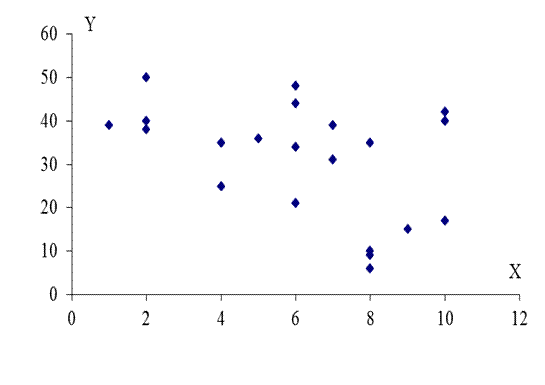
Рисунок 10 – График двумерного рассеяния
(X – уровень соперничества, Y – либеральный стиль общения)
Рассчитаем коэффициент корреляции по указанной выше формуле. Результаты представлены в таблице 7.
Таблица 7 – Коэффициент корреляции Пирсона
между стилем общения и уровнем соперничества
| Стиль общения | Коэффициент корреляции Пирсона стиля общения с уровнем соперничества |
| Деспотический | 0, 993 |
| Коллегиальный | -0, 053 |
| Либеральный | -0, 441 |
Так как количество респондентов N =21, то число степеней свободы  . Из таблицы «Значения (критические) коэффициента корреляции Пирсона r для различный уровней зависимости и различного числа степеней свободы (размеров выборок)» (см. приложения) найдем критические значения коэффициента корреляции и выпишем их в таблицу 8.
. Из таблицы «Значения (критические) коэффициента корреляции Пирсона r для различный уровней зависимости и различного числа степеней свободы (размеров выборок)» (см. приложения) найдем критические значения коэффициента корреляции и выпишем их в таблицу 8.
Таблица 8 – Критические значения коэффициента корреляции Пирсона (для N =21)
| Число степеней свободы df=(N-2) | Уровень значимости для двустороннего критерия Пирсона | ||||
| 0, 050 | 0, 250 | 0, 010 | 0, 005 | 0, 0005 | |
| 0, 369 | 0, 430 | 0, 050 | 0, 549 | 0, 6652 |
Таким образом, из таблицы 7 и 8 видно, что между уровнями соперничества и деспотическим стилем общения наблюдается линейная корреляция по Пирсону на уровне значимости 0, 0005, т.е. с надежностью 99, 95% можно утверждать, что люди, склонные к соперничеству предпочитают деспотичный стиль общения. Гипотеза о корреляции коллегиального стиля общения с уровнем соперничества и корреляции либерального стиля общения с уровнем соперничества на уровне значимости 0, 05 статистически не подтвердились.
4. Анализ классификации при сравнении эмпирического и теоретического распределений
Проведено исследование, в котором проводилось сравнение частот проявления агрессии в группе студентов-психологов и остальных студентов вуза в ходе проведения тренинга преодоления агрессивного поведения. Средняя частота проявления агрессии по вузу составила K %, а в данном случае из N студентов-психологов ярко выраженное агрессивное поведение проявили L студентов. Можно ли на этом основании сделать вывод о том, что среди студентов психологов проявление агрессии наблюдается реже, чем в целом по вузу? (Значения N, K, L см. в таблице 9).
Таблица 9 – Значения N, K, L согласно варианту контрольной работы
| N | K | L |
Цель задания. Освоение метода анализа классификации при сравнении эмпирического и теоретического распределений в случае двух градаций (применяется биноминальный критерий) и в случае более двух градаций (применяется критерий χ 2).
Решение. Сформулируем гипотезы:
- H0: Частота проявления агрессии в группе студентов-психологов не превышает средней частоты проявления агрессии в целом по вузу;
- H1: Частота проявления агрессии в группе студентов-психологов превышает среднюю частота проявления агрессии в целом по вузу.
Будем считать, что вероятность проявления агрессии у студентов совпадает с частотой его проявления у всех студентов вуза 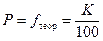 . Используя данные таблицы 9, найдем эмпирическую частоту проявления агрессии у студентов-психологов по формуле
. Используя данные таблицы 9, найдем эмпирическую частоту проявления агрессии у студентов-психологов по формуле  . Таким образом, получаем
. Таким образом, получаем
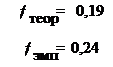
Так как: 1) f эмп > f теор, 2) 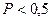 , 3) объем выборки
, 3) объем выборки 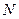 удовлетворяет условию:
удовлетворяет условию: 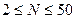 , то применим биномиальный критерий. Согласно биномиальному критерию подтверждается гипотеза H1: f эмпдостоверно выше f теор.
, то применим биномиальный критерий. Согласно биномиальному критерию подтверждается гипотеза H1: f эмпдостоверно выше f теор.
Таким образом, частота проявления агрессии в исследуемой группе студентов-психологов превышает среднюю частота проявления агрессии в целом по вузу.
5. Анализ таблиц сопряженности двух номинативных признаков
Цель задания: освоение метода анализа таблиц сопряженности.
Для каждого абитуриента репрезентативной выборки определены а) пол; б) одна из четырех возможных новых гуманитарных специальностей открытых только в данном вузе (таблица 10).
Таблица 10 – Таблица сопряженности двух номинативных признаков
согласно варианту контрольной работы
| Y – специальность | |||||||
| Всего | |||||||
| Х - пол | Муж. (1) | ||||||
| Жен. (2) | |||||||
| Всего: |
Проверить гипотезу о зависимости выбора специальности от пола.
Решение. Сформулируем гипотезы:
- H0: Распределение абитуриентов по заданным гуманитарным специальностям открытым в вузе не зависит от их пола;
- H1: Распределение абитуриентов по заданным гуманитарным специальностям открытым в вузе зависит от их пола.
Для проверки гипотезы H0 будем использовать метод, получивший название c2 (хи-квадрат) критерий.
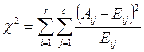
где 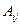 – фактическая частота в i-ой строке, j-ом столбце таблицы сопряженности;
– фактическая частота в i-ой строке, j-ом столбце таблицы сопряженности;
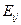 – ожидаемая частота в i-ой строке, j-ом столбце таблицы сопряженности;
– ожидаемая частота в i-ой строке, j-ом столбце таблицы сопряженности;
r = число строк в таблице сопряженности;
c = число столбцов в таблице сопряженности.
Найдем фактические частоты, которые находятся делением значения, записанного в соответствующей ячейке таблицы на общее число наблюдений (число в правом нижнем углу таблицы). Результаты запишем в таблицу 11.
Таблица 11 – Таблица фактических частот заданных номинативных признаков
| Y – специальность | |||||||
| Всего | |||||||
| Х - пол | Муж. (1) | ||||||
| Жен. (2) | |||||||
| Всего: |
Теперь найдем ожидаемые частоты, которые находятся делением произведения двух соответствующих этой клетки сумм, записанных по краям таблицы, на сумму всех наблюдаемых частот. Результаты запишем в таблицу 12.
Таблица 12 – Таблица ожидаемых частот заданных номинативных признаков
| Y - специальность | |||||||
| Всего | |||||||
| Х - пол | Муж. (1) | ||||||
| Жен. (2) | |||||||
| Всего: |
Вычисленную величину c2 сравним со стандартными значениями. Если она превышает то или иное стандартное значение, исходная гипотеза о независимости признаков отвергается на соответствующем уровне значимости. Для этого найдем число степеней свободы. В случае, когда по каждому признаку подразделяют не менее трёх градаций, число степеней свободы находят по формуле: n = (r - 1) + (c -1), где r - число градаций в первой классификации, c - во второй классификации. Если же одна из классификаций содержит только две градации, то n = (c – 1), где с – число градаций в более дробной классификации.
Таблица 13 – Стандартные значения распределения c2
| Число степеней свободы | Уровень значимости | |||||
| 0, 01 | 0, 025 | 0, 05 | 0, 95 | 0, 975 | 0, 99 | |
| 9, 2 | 7, 4 | 0, 103 | 0, 051 | 0, 02 | ||
| 11, 3 | 9, 4 | 7, 8 | 0, 352 | 0, 216 | 0, 115 | |
| 13, 3 | 11, 1 | 9, 5 | 0, 711 | 0, 484 | 0, 297 | |
| 15, 1 | 12, 8 | 11, 1 | 1, 15 | 0, 831 | 0, 554 |
Так как число степеней свободы здесь равно n = 4 – 1 = 3 фактическая величина 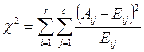 = 2, 48 меньше представленных в таблице критических значений для уровней значимости 0, 01; 0, 025 и 0, 05, следовательно гипотеза Н0 о независимости распределения абитуриентов по заданным гуманитарным специальностям открытым в данном вузе от пола отвергается, а принимается гипотеза Н1.
= 2, 48 меньше представленных в таблице критических значений для уровней значимости 0, 01; 0, 025 и 0, 05, следовательно гипотеза Н0 о независимости распределения абитуриентов по заданным гуманитарным специальностям открытым в данном вузе от пола отвергается, а принимается гипотеза Н1.
Таким образом, рассматриваемое в задание распределение абитуриентов по заданным гуманитарным специальностям, открытым в данном вузе статистически значимо зависит от пола абитуриентов.
6. Анализ последовательности (критерий серий)
Цель задания: освоение метода анализа последовательности с помощью критерия серий.
Исследуется динамика научения в игровом задании. Исследователь предполагает частые повторы проигрышей в начале и выигрышей – в конце последовательности игр (проверяется направленная гипотеза). Игроком сыграно N партий, из них проиграно M, выиграно L, число серий W. К концу последовательности игр наблюдается преобладании выигрышей. Проверить гипотезу с применением Z-критерия серий.
Таблица 1 – Значение числа партий, выигрышей, проигрышей и серий
| N | M | L | W |
Решение. Сформулируем гипотезы:
- H 0: Выигрыши и проигрыши случайны;
- H 1: В последовательности выигрышей и проигрышей существует значимая статистическая зависимость – число выигрыше в конце последовательности преобладает перед числом проигрышей (направленная гипотеза).
Для проверки гипотезы H0 будем использовать метод, получивший название критерий серий для одной выборки. Критерий серий позволяет с определенной долей вероятности ответить на вопрос, существует ли зависимость в последовательности выигрышей и проигрышей.
Уровень значимости выберем 0, 05.
Последовательность может оказаться неслучайной, если в ней слишком мало или слишком много серий. Поэтому из таблицы критических значений критерия серий находим два критических значения: R верх=21, R нижн = 9, – верхнюю и нижнюю границу соответственно. Если W больше либо равно верхней границы или меньше либо равно нижней границы, то гипотезе H 0 отклоняется. Так как число серий W=8, заданное в условии задачи, меньше R нижн=9 то гипотеза H 0 о случайности выигрышей и проигрышей не подтвердилась.
Таким образом, в последовательности выигрышей и проигрышей существует значимая (на уровне значимости 0, 05) статистическая зависимость – число выигрыше в конце последовательности партий преобладает перед числом проигрышей. Следовательно, можно сделать вывод о статистически значимой динамике научения в игровом задании.
Заключение
В контрольной работе было проведено:
- изучение методов анализа эмпирических данных на основе расчета частот, построения гистограмм и графиков распределения, вычисления выборочных средних, дисперсии и стандартного отклонения;
- изучение методов проверки распределения эмпирических данных на нормальность (метод анализа асимметрии и эксцесса, графический метод, критерий Колмогорова – Смирнова);
- изучение методов проверки корреляционной зависимости между двумя признаками (линейная корреляция Пирсона);
- изучение методов проверки критериев согласия (биномиальный критерий);
- изучение методов анализа таблиц сопряженности критерием 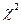 ;
;
- изучение метода анализа последовательности – критерия серий.
Иногда можно слышать утверждения, что научный подход с применением математических методов необходим для академических научных исследований, а в практической работе вполне достаточно здравого смысла. Да, практическая деятельность психолога – это, прежде всего, искусство применения практических методов. Но здравого смысла недостаточно для профессиональной работы. Профессионал отливается тем, что может обосновать свою точку зрения, скажем, проверить эффективность того или иного практического метода или состоятельности организационного решения. При этом он будет опираться на научно обоснованные аргументы, а не только на собственное субъективное мнение.
В результате можно сделать следующие выводы по контрольной работе:
- психология в любых ее приложениях – и практических, и теоретических, может развиваться только на основе количественных исследований, связывающих теорию и практику с фактами;
- неотъемлемой частью подготовки полноценного специалиста-психолога является изучение не только экспериментальной психологии, но и математических методов психологического исследования.
Таким образом, задачи контрольной работы выполнены, и цель достигнута.