Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Исследование нормальности распределения
|
|
По методике Цунга была исследована группа студентов факультета психологии. Измерялся уровень депрессивного состояния. (Результаты исследований для каждого варианта представлены в таблице ниже). Построить кривую распределения уровня депрессивного состояния у студентов-психологов. Отличается ли распределение признака от нормального?
Цель задания. Расчет асимметрии и эксцесса. Освоение метода проверки отклонения распределения от нормального с помощью параметров асимметрии и эксцесса, графически, а также с помощью критерия Колмогорова-Смирнова.
Таблица 4 – Результаты измерений депрессивного состояния
Группа студентов факультета психологии по методике Цунга
| Результаты измерений |
Решение. Для решения задачи перенесем данные из таблицы 4 на лист рабочей книги MS Excel.
а) Используя следующие формулы для заданной выборки найдем асимметрию А
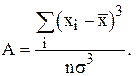
и эксцесс Е
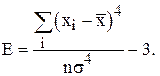
В результате получаем следующие значения асимметрии и эксцесса:
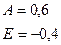
Для проверки нормальности распределения по значениям асимметрии и эксцесса найдем для них критические значения по формулам:
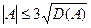
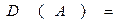
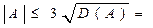
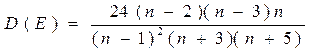
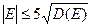
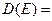
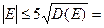
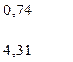
Таким образом, т.к. найденные значения асимметрии и эксцесса не превышают по модулю своих критических значений, то распределение можно считать нормальным.
б) Проверим с помощью критерия Колмогорова-Смирнова гипотезу о том, что эмпирические данные, представленные в таблице 5, подчиняются нормальному распределению при уровне значимости a =0, 1.
Статистика Колмогорова для проверки гипотезы H 0 против двусторонней альтернативы определяется как максимум модуля отклонения эмпирической функции распределения F’ (x) от гипотетической F (x).
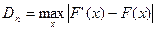
А.Н. Колмогоров доказал, что какова бы ни была функция распределения F (x) величины Х при неограниченном увеличении количества наблюдений n функция распределения случайной величины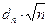 
асимптотически приближается к функции распределения 
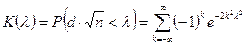. Иначе говоря, этот критерий характеризует вероятность того, что величина 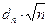не будет превосходить параметр l для любой теоретической функции распределения. Уровень значимости a выбирается из условия 
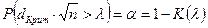. Результаты расчетов представим в таблице 7.
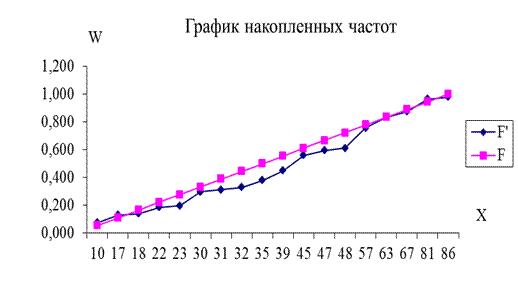
Рисунок 7 – График накопленных частот
Таблица 5 – Расчеты эмпирический и теоретических накопительных частот
| i | X | Эмпирически накопленная частота F' | Теоретическая накопленная частота F | F'-F | |F'-F| |
| 0, 075 | 0, 056 | 0, 019 | 0, 019 | ||
| 0, 131 | 0, 111 | 0, 019 | 0, 019 | ||
| 0, 140 | 0, 167 | -0, 026 | 0, 026 | ||
| 0, 185 | 0, 222 | -0, 037 | 0, 037 | ||
| 0, 197 | 0, 278 | -0, 080 | 0, 080 | ||
| 0, 297 | 0, 333 | -0, 036 | 0, 036 | ||
| 0, 313 | 0, 389 | -0, 076 | 0, 076 | ||
| 0, 329 | 0, 444 | -0, 115 | 0, 115 | ||
| 0, 380 | 0, 500 | -0, 120 | 0, 120 | ||
| 0, 451 | 0, 556 | -0, 105 | 0, 105 | ||
| 0, 559 | 0, 611 | -0, 052 | 0, 052 | ||
| 0, 595 | 0, 667 | -0, 072 | 0, 072 | ||
| 0, 612 | 0, 722 | -0, 110 | 0, 110 | ||
| 0, 756 | 0, 778 | -0, 021 | 0, 021 | ||
| 0, 833 | 0, 833 | 0, 000 | 0, 000 | ||
| 0, 875 | 0, 889 | -0, 014 | 0, 014 | ||
| 0, 963 | 0, 944 | 0, 018 | 0, 018 | ||
| 0, 978 | 1, 000 | -0, 022 | 0, 022 |
Max |F'-F|= 1, 20
Из таблицы распределения при a =0, 1 найдем l =1, 22. Для n = 18 критическое значение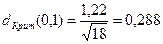 
. Поскольку величина 
= 
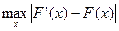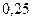меньше критического значения 0, 288, гипотеза о принадлежности выборки нормальному закону не отвергается.
Построим график накопленных частот (рис. 8). Из графика видно, что эмпирические данные правой части распределения довольно близко расположены к линии нормального распределения.
Таким образом, проверка полученных эмпирических данных на нормальность с помощь расчета асимметрии, эксцесса и графически с использованием критерия Колмогорова-Смирнова дала положительный результат. В целом, с надежностью 98% можно утверждать, что эмпирическое распределение является нормальным.