Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Логические языки
|
|
Логические языки и математические языки используют разную парадигму подхода.
Аристотель 5 век до н. э.
Сущность - все то, о чем можно утверждать.
Классы сущностей - совокупности объединенные с помощью общего имени.
Квантор всякий - то что верно для всех сущностей класса.
Квантор некоторый - то что верно для подкласса.
С помощью квантов строятся базовые системы утверждений: S P (субъект-предикат)
Из набора утверждений можно делать выводы(посылки-> результирующие)
Количество посылок соответствует рангу вывода.
Выводы ранга 0 - законы силлогистики (тождества[сущность из класса обладает всеми свойствами класса], противоречия[нельзя входить и не входить в класс], закон исключенного третьего[сущность либо входит в класс либо не входит]).
Выводы ранга 2 называются силлогизмы Аристотеля: Меньший термин, Средний термин, Больший термин
Имеются правильные и не правильные модусы силлогизма, а именно только 24 из 256 являются правильными без относительных содержаний.
Правильные модусы образуют ядро теории дедуктивных выводов, где от правильных посылок образуются правильные выводы.
На этой основе были созданы две мощные формальные системы которые позволили автоматизировать рассуждения опираясь на ядро теории дедуктивных выводов, где от правильных посылок образуются правильные выводы.
---
Как правило тонкие оттенки смысла не передаются.
Не существуют способы в математическом смысле доказать что перевод ЕЯ-ПОЯ неадекватные.
Введем понятие сущности. Под сущностью будем понимать все то, о чем можно нечто утверждать. Под это понятие подходят объекты окружающего нас мира, явления его, протекающие в нем процессы, окружающие нас субъекты, включая нас самих. Вообще, все, о чем что-то можно говорить на естественном языке. Сущности могут образовывать классы — совокупности, объединенные с помощью общего имени. При этом отдельные сущности могут иметь уникальные собственные имена*. Для обозначения классов сущностей будем использовать традиционные буквы S, Р и М, а для обозначения конкретных сущностей — малые латинские буквы а, b и т. д.
* Учение об именовании (номинации) — одна из обширных и сложных областей логики. В этой книге мы используем термины, касающиеся имен, во многом опираясь на интуитивные представления
Введем еще два квантора: всякий и некоторый. Первый из них, будучи поставлен рядом с именем класса, показывает, что в высказывании будет утверждаться нечто, что одновременно истинно для всех сущностей, входящих в этот класс. Если класс пуст, т. е. не содержит конкретных сущностей, то высказывание говорит о пустом классе. Например, «Всякий демон способен сжимать и растягивать время», если не верить в существование демонов, есть высказывание о пустом классе. Однако, несмотря на то, что класс демонов пуст, высказывание все-таки обладает определенным смыслом, понятным каждому человеку. Во всяком случае, человек всегда может себе представить воображаемый мир, в котором демоны не только существуют, но и являются важными действующими персонажами этого мира.
Чистая игра с именами несуществующих сущностей часто нравится людям, особенно детям.
Вторым квантором в силлогистике Аристотеля является квантор «некоторый». Если он поставлен рядом с именем некоторого класса сущностей, то это означает, что в высказывании, будет нечто утверждаться относительно какого-то подкласса сущностей, входящих в данный класс. Этот подкласс может сливаться со всем классом или содержать единственную конкретную сущность из исходного класса. Важно только условие непустоты этого подкласса, если исходный класс не пуст. А если он пуст, то подкласс образуют мыслимые конкретные сущности. В высказывании «Некоторые демоны слушали музыку внимательно» в воображаемом классе сущностей с именем «демоны» речь идет о некотором подклассе.
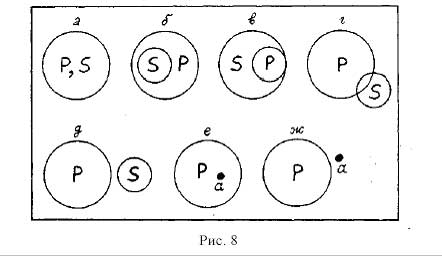
С помощью кванторов строятся шесть схем базовых высказываний, используемых в силлогистике.
1. Всякий S есть Р.
2. Всякий S не есть Р.
3. Некоторый S есть Р.
4. Некоторый S не есть Р.
5. S есть Р.
6. S не есть Р.
Отметим, что если S определяет сущности, о которых что-то утверждается в высказывании, то Р определяет, что именно о них говорится. Кванторы выделяют тот подкласс сущностей, о которых идет речь. Поэтому иногда S называют субъектом высказывания, а Р — предикатом высказывания.
Мы эти термины в дальнейшем использовать не будем.
Если высказывания 1—4 относятся к некоторым утверждениям о принадлежности или непринадлежности множеств элементов некоторому классу элементов, обладающих свойством Р, то высказывания 5 и 6 имеют несколько иную природу. Высказывание 5 утверждает, что класс S совпадает с классом элементов, обладающих свойством Р, а высказывание 6 говорит о том, что эти классы не совпадают.
Для индивидуальных конкретных сущностей имеются две схемы базовых высказываний.
7. а есть Р.
8. а не есть Р.
В силлогистике Аристотеля двух последних высказываний не было. Мы их приводим для полноты картины.
В приведенных восьми схемах базовых высказываний имеется один элемент, который мы пока не объяснили. Он представлен связками «есть» и «не есть». К сожалению, в русском языке эти связки не имеют однозначного смыслового значения. Следующие примеры иллюстрируют это: «Треугольник есть многоугольник», «Фигура АВС есть прямоугольный треугольник», «Сумма квадратов катетов есть квадрат гипотенузы», «Причина есть». В этих четырех примерах связка «есть» используется в четырех различных смыслах. В первом предложении говорится о включении одного множества сущностей в другое. В теории множеств этот случай задается с помощью отношения S " вложено в" Р. Во втором случае «есть» трактуется как отношение принадлежности элемента множеству, т.е. как а " является элементом" Р. В третьем высказывании вместо «есть» подразумевается знак равенства, а в последнем случае «есть» определяет лишь фиксацию наличия сущности «причина». Ясно, что при такой неоднозначности невозможно построить строгую теорию.