Исчисление высказываний

К первоначальным, неопределяемым понятиям аксиоматической теории высказываний относятся следующие: 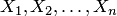— пропозициональные переменные; 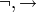— логические связки; 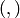— технические знаки. Первоначальным понятием является также понятие формулы, которое определяется (как и в алгебре высказываний, см. определение 2.1) индуктивным образом:

1) каждая пропозициональная переменная есть формула;
2) есл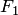и и 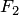— формулы, то выражения 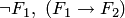также являются формулами;
3) никаких других формул, кроме получающихся согласно пунктам 1 и 2 нет.

Следующий шаг в построении аксиоматической теории высказываний состоит в выборе системы аксиом. В качестве аксиом выбираются формулы следующих видов:

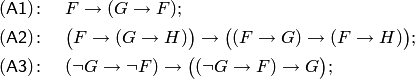
где 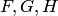— произвольные формулы. Таким образом, каждое из выражений 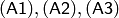задает лишь форму аксиомы. Они превращаются в аксиомы, если вместо 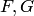и 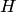подставить конкретные формулы (в частности, пропозициональные переменные). Следовательно, каждое из этих выражений задает бесконечное множество формул. Все они называются аксиомами. Поэтому каждое из выражений 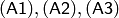называют схемой аксиом.

Наконец, заключительный шаг, закладывающий основу аксиоматической теории высказываний, состоит в выборе правил вывода. Единственным правилом вывода будет служить правило заключения (или отделения, или modus ponens, или сокращенно 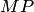): из формул 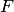и 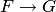непосредственно следует формула .

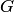Как и в алгебре высказываний, внешние скобки у формулы принято не писать.

Поскольку в аксиомах не участвуют связки 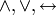, то их придется определить. Введем следующие определения:

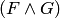означает ;
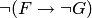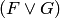означает ;
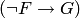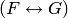означает .

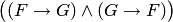Смысл, например, первого из определений состоит в том, что, каковы бы ни были формулы 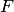и 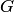, формула 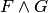служит обозначением для формулы .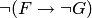