Относительный покой жидкости: горизонтальное перемещение жидкости с постоянным ускорением

При движении сосуда в горизонтальном направлении с постоянным ускорением (рис. 2.5) на жидкость, находящуюся в нем, действует сила тяжести и сила инерции.

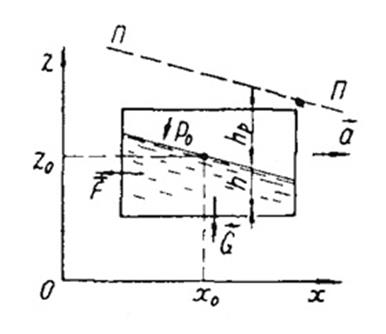
Рисунок 2.5 Горизонтальное перемещение резервуара с жидкостью

В этом случае имеем: ; ; .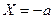

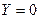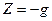Поверхность равного давления при этом определяется уравнением:

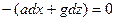. (2.19)

После интегрирования получаем:

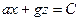. (2.20)

или

. (2.21)

Поверхностями равного давления будут плоскости, углы наклона которых к горизонтальной плоскости определяются угловым коэффициентом, равным ().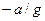

Закон распределения давления можно получить после интегрирования уравнения (2.6) с учетом 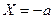; ; 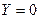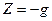, а также граничных условий 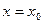; ; 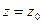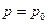, в следующем виде:

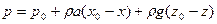. (2.22)

Данное уравнение показывает, что при движении резервуара с жидкостью вдоль горизонтальной плоскости с постоянным ускорением 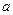распределение давления подчиняется линейному закону для любой фиксированной вертикали (, ,...).

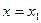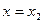Сила давления на криволинейную поверхность (рис. 2.6) может быть найдена из условия динамического равновесия объема жидкости , заключенного между криволинейной поверхностью и плоскостью, проведенной через граничный контур поверхности (на рис. 2.6 этот объем заштрихован):

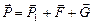, (2.23)

где 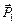- сила давления на плоское сечение АВ, определяемая по формуле ;

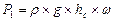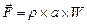- сила инерции;

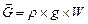- вес объема жидкости.

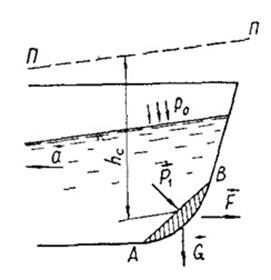
Рисунок 2.6 - К определению силы давления на криволинейную поверхность