
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Лабораторна робота №2.
|
|
Операції з масивами даних в інформаційних системах менеджменту.
Часто при работе с массивами приходится применять одну и туже операцию к целому диапазону ячеек или произвести расчет по формулам зависящим от большого массива данных. Для решения подобных задач Excel предоставляет простые и удобные средства, которые будут описаны далее.
1. Простейшие операции над массивами.
В качестве первого примера простой операции рассмотрим умножение массива А1: В2 на число 5. Выделите на рабочем листе область, например D1: E2, такого же размера, как массив – множимое (Рис.2.1),
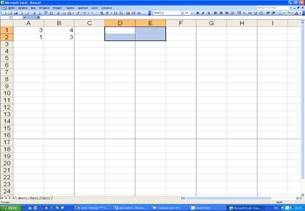
Рис.2.1. Выделение диапазона для ввода результирующего массива.
Теперь введите формулу «= А1: В2*5».
Для этого установите курсор в строке формула и закончите ввод не нажатием, клавиши «Enter», как обычно, а нажатием «Ctrl+Shift+ Enter». Таким образом вы сообщите программе, что необходимо выполнить операцию над массивом. При этом Excel заключит формулу в строке формула в фигурные скобки (Рис.2.2.)
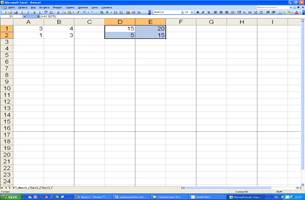
Рис.2.2. Произведение массива на число.
При работе с массивами формула действует на все ячейки диапазона. Нельзя изменять отдельные ячейки в операндах формулы.
2. Встроенные функции для роботы с матрицами
В Excel имеются следующие специальные функции для роботы с матрицами
МОБР (MINVERSE) Обратная матрица
МОПРЕД (MDETTRM) Определитель матрицы
МУМНОЖ (MMULT) Матричное произведение двух матриц
ТРАНСП (TRANSPOSE) Транспонированная матрица
Во всех случаях при роботе с матрицами перед вводом формулы надо выделить область на рабочем листе, куда будет выведен результат исчислений.
Решим в качестве примера систему линейных уравнений с двумя неизвестными, матрица коэффициентов которой записана в ячейках F1: G2, а свободные члены - в ячейки I1: I2(рис.2.3)
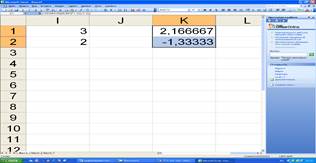
Рис.2.3. Решение системы линейных уравнений.
Для решения этой задачи вспомним, что решение линейной системы АХ = В, где А - матрица коэффициентов, В - столбец (вектор свободных членов, Х - столбец (вектор) – неизвестных, имеет вид Х=А-1В, где А-1 – матрица обратная по отношению к матрице А. Поэтому для решения нашей системы уравнений выделим под вектор решений диапазон К1: К2 и введем в него формулу, как показано на рис.2.2.
Решим также систему линейных уравнений А2Х=В
Для решения этой системы введем в диапазон ячеек А1: В2 элементы матрицы А, а в диапазон ячеек D1: D2 – элементы столбца свободных членов В. Выберем диапазон F1: F2, куда поместим элементы вектора решения и введем следующую формулу:
{=МУМНОЖ(МОБР(МУМНОЖ(А1: В2; А1: В2)); D1: D2)}
Рассмотрим пример вычисления квадратичной формы z = ХтАХ, где А – квадратная матрица, введенная в диапазон А1: В2, Х – вектор, введенный в диапазон D1: D2, а символ (т) обозначает операцию транспонирования. Для вычисления z введем в ячейку F1 формулу:
{=МУМНОЖ(МУМНОЖ(ТРАНСП(D1: D2); А1: В2); D1: D2)}
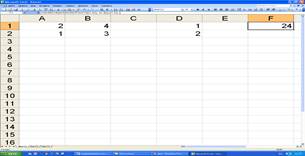
Рис.2.4. Нахождение квадратичной формы.
Вычислим значение квадратичной формы z=YTATAY.
Для решения этой задачи введем в диапазон ячеек А1: В2 элементы матрицы А, а в диапазон ячеек D1: D2 – элементы столбца Y. Для вычисления квадратичной формы введем в ячейку F1 формулу:
{=МУМНОЖ(ТРАНСП(D1: D2); МУМНОЖ(ТРАНСП(А1: В2); МУМНОЖ (А1: В2; D1: D2)))}