
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Завдання.
|
|
1.Скориставшись рисунком 8, визначити область зміни коефіцієнта с2, в якій точка С як і раніше залишатиметься єдиною оптимальною точкою. Вихідне значення с1 = 3 залишити незмінним.
2.Визначити оптимальні кутові точки для випадку, коли значення с2 починає перевищувати отримане в п.1 максимальне значення.
3.Нехай цільова функція F=3x1+2x2 замінена на F=3x1+x2. В цьому випадку оптимальною кутовою точкою буде точка В з координатами х1=4 і х2=0. Це означає, що кукурудзу виробляти недоцільно. При якій ціні на пшеницю стане вигідним виробництво кукурудзи?
ВІДПОВІДІ:
1. 3/2 < с2 < 6.
2. Точка D.
3. При ціні, що не перевищує 2 тис. грн. за одну тонну (початкова ціна 3 тис. грн).
АНАЛІЗ МОДЕЛЕЙ НА ЧУТЛИВІСТЬ ПО ОСТАННІЙ
(ОПТИМАЛЬНІЙ) СИМПЛЕКС-ТАБЛИЦІ.
Крім розв′ язання задачі ЛП графічним методом, оптимальне рішення можна знайти і іншим, хоч і менш раціональним методом: обчислити координати всіх вузлових точок багатокутника допустимих значень і підрахувати в цих точках значення цільової функції. Порівнюючи набуті значення, знайти максимальне і мінімальне значення, тобто екстремуми цільової функції. На цьому принципі заснований метод, який називається симплекс-методом розв′ язання задач лінійного програмування.
Розв′ язавши задачу цим методом, завершальну симплекс-табліцу можна використовувати для аналізу на чутливість. З неї або безпосередньо, або за допомогою простих додаткових обчислень можна отримати інформацію відносно:
1) оптимального рішення;
2) статусу ресурсу;
3) цінності кожного ресурсу;
4) чутливості оптимального рішення до зміни запасів ресурсів, варіацій коефіцієнтів цільової функції і інтенсивності споживання ресурсів.
Відомості, що відносяться до перших трьох пунктів, можна отримати безпосередньо з симплекс-таблиці для оптимального рішення. Отримання інформації, що відноситься до четвертого пункту, вимагає додаткових обчислень.
Розв′ яжемо дану задачу симплекс-методом. Для цього цільову функцію і систему обмежень запишемо в канонічному вигляді:
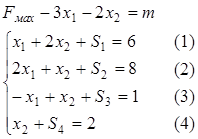 або
або 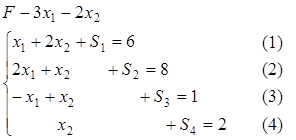
і виконаємо ряд ітерацій:
0 ітерація – вихідні дані
| F | x1 | x2 | S1 | S2 | S3 | S4 | рішення | відношення | |
| F | –3 | –2 | |||||||
| S1 | 6/1=6 | ||||||||
| S2 | 8/2=4 | ||||||||
| S3 | –1 | ||||||||
| S4 |
1 ітерація – зміна однієї базової змінної
| F | x1 | x2 | S1 | S2 | S3 | S4 | рішення | відношення | |
| F | –1/2 | 3/2 | |||||||
| S1 | 3/2 | –1/2 | 4/3 | ||||||
| x1 | 1/2 | 1/2 | |||||||
| S3 | 3/2 | 1/2 | 10/3 | ||||||
| S4 |
2 (завершальна) ітерація - зміна другої базової змінної
| F | x1 | x2 | S1 | S2 | S3 | S4 | рішення | відношення | |
| F | 1/3 | 4/3 | 38/3 | ||||||
| x2 | 2/3 | –1/3 | 4/3 | ||||||
| x1 | –1/3 | 2/3 | 10/3 | ||||||
| S3 | –1 | ||||||||
| S4 | –2/3 | 1/3 | 2/3 |