
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Максимальна зміна запасу ресурсу.
|
|
Припустимо, що в задачі про ферму запас ресурсу «1» змінився на D1 тобто запас продукту b1 складе Db1=(b1)*-(b1)** = (6+D1) га.
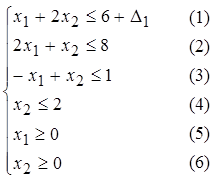
У вихідній симплекс-таблиці це приведе тільки до зміни комірки на перетині рядка S1 і стовпчика «рішення»
0 ітерація
| F | x1 | x2 | S1 | S2 | S3 | S4 | рішення | |
| F | –3 | –2 | ||||||
| S1 | 6 + D1 | |||||||
| S2 | ||||||||
| S3 | –1 | |||||||
| S4 |
Якщо виконати всі алгебраїчні перетворення, що відповідають послідовності ітерацій, то виявиться, що на кожній ітерації D1 буде впливати тільки на праві частини обмежень, і завершальна симплекс-таблиця матиме вигляд:
| F | x1 | x2 | S1 | S2 | S3 | S4 | рішення | |
| F | 1/3 | 4/3 | 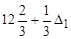
| |||||
| x2 | 2/3 | –1/3 | 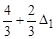
| |||||
| x1 | –1/3 | 2/3 | 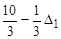
| |||||
| S3 | –1 | 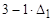
| ||||||
| S4 | –2/3 | 1/3 | 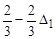
|
Можна побачити, що в завершальній симплекс-таблиці рішення зміниться на величину, пропорційну приросту D1, а коефіцієнт пропорційності рівний коефіцієнту, взятому в стовпчику (S1) для рядка відповідної змінної.
Треба відзначити, що, аналогічно міркуючи, можна отримати відповідні результати і для інших обмежень (b2, b3, b4). Іншими словами, при аналізі впливу зміни в правих частинах (2), (3) і (4) обмежень потрібно користуватися коефіцієнтами при змінних S2, S3 і S4 відповідно.
З отриманих результатів можна зробити наступні висновки. Оскільки введення D1 позначається лише на правій частині симплекс-таблиці, та зміна запасу ресурсу може вплинути тільки на допустимість рішення.
| F | x1 | x2 | S1 | S2 | S3 | S4 | рішення | |
| x2 | 2/3 | –1/3 | 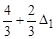
| |||||
| x1 | –1/3 | 2/3 | 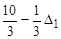
| |||||
| S3 | –1 | 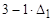
| ||||||
| S4 | –2/3 | 1/3 | 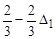
|
Пригадаємо, що кожен рядок симплекс-таблиці є рівняння, записане у вигляді таблиці, наприклад, перший рядок це рівняння
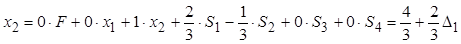 або
або 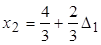 .
.
Слід пам'ятати, що задача ЛП вирішується в припущенні, що будь-яка змінна не може приймати від′ ємних значень. З цього виходить, що величина D1 повинна бути обмежена таким інтервалом значень, при яких виконується умова невід′ ємності правих частин обмежень в результуючій симплекс-таблиці. А саме:
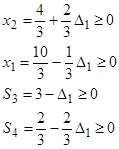 Þ
Þ 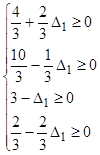 Þ
Þ 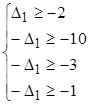 Þ
Þ 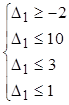 Þ
Þ 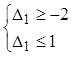 .
.
Розв′ язавши систему нерівностей, ми знайдемо інтервал зміни першого ресурсу (площа), для якого рішення даної задачі буде допустимим: 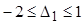 . Будь-яке значення D1, що виходить за межі вказаного інтервалу, тобто зменшення площі, що засівається, більш ніж на 2 га або збільшення більш ніж на 1 га, приводить до неприпустимості рішення і нової сукупності базисних змінних. Даний інтервал зміни D1 відповідає інтервалу зміни самого ресурсу Db1, а саме b1** ≤ Db1 ≤ b1* або 6-2 ≤ Db1 ≤ 6+1, що рівнозначно 4 ≤ Db1 ≤ 7.
. Будь-яке значення D1, що виходить за межі вказаного інтервалу, тобто зменшення площі, що засівається, більш ніж на 2 га або збільшення більш ніж на 1 га, приводить до неприпустимості рішення і нової сукупності базисних змінних. Даний інтервал зміни D1 відповідає інтервалу зміни самого ресурсу Db1, а саме b1** ≤ Db1 ≤ b1* або 6-2 ≤ Db1 ≤ 6+1, що рівнозначно 4 ≤ Db1 ≤ 7.
Висновок: З метою збільшення доходу площа під сільгосп-культурами може бути збільшена до 7 га. Більш того, за якихось причин ця площа може зменшитися до 4 га (хоча це небажано), проте, якщо ця зміна лежатиме у вказаних межах, статус ресурсів не зміниться.
5. Максимальна зміна коефіцієнтів питомого прибутку (вартості).
Встановимо інтервали допустимих змін коефіцієнтів цільовій функції (вартість), розглядаючи кожний з коефіцієнтів окремо, для яких оптимальне значення змінних залишаються незмінними.
Припустимо, що прибуток від виробничої діяльності, що асоціюється зі змінною х1, змінюється на d1, тобто ставши с1* = 3 + d1, при незмінному с2 = 2 (d1 може бути як від′ ємною так і невід′ ємною). Цільова функція в цьому випадку приймає вигляд: 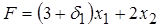 і вихідна симплекс-таблиця матиме вигляд:
і вихідна симплекс-таблиця матиме вигляд:
| F | x1 | x2 | S1 | S2 | S3 | S4 | рішення | |
| F | –3–d1 | –2 | ||||||
| S1 | ||||||||
| S2 | ||||||||
| S3 | –1 | |||||||
| S4 |
Слід зазначити, що рівняння цільової функції також ніколи не використовується як провідне рівняння. Тому будь-які зміни коефіцієнтів цільовій функції зроблять вплив тільки на F-рівняння результуючої таблиці. Це приведе до того, що коефіцієнти в F-рядку результуючої таблиці зміняться на величину пропорційну d1 (див. табл. 5). Коефіцієнтом пропорційності є коефіцієнт при відповідних змінних в рядку для змінної х1 (адже саме для цієї змінної ми розглядаємо межі зміни коефіцієнта).
Розглянута задача є задачею на відшукання максимуму, тому по умові оптимальності всі коефіцієнти в F-рівнянні повинні бути невід′ ємними. Запишемо цю умову у вигляді системи нерівностей:
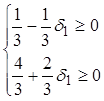 Þ
Þ 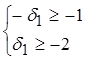 Þ
Þ 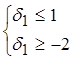 .
.
Цю систему нерівностей можна записати у вигляді подвійної нерівності 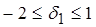 , тобто
, тобто 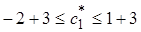 або
або 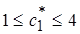 .
.
Таблиця 5
| F | x1 | x2 | S1 | S2 | S3 | S4 | рішення | |
| F | 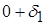
| 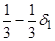
| 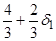
| 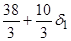
| ||||
| x2 | 2/3 | –1/3 | 4/3 | |||||
| x1 | –1/3 | 2/3 | 10/3 | |||||
| S3 | –1 | |||||||
| S4 | –2/3 | 1/3 | 2/3 |
Таким чином, якщо ситуація на ринку зміниться і закупівельні ціни на пшеницю (х1) зміняться, а саме зменшуться до 1 або збільшаться до 4, дохід (F) хоч і зміниться, але все одно визначатиметься дефіцитними ресурсами: площа землі і трудові ресурси. Користуючись останньою таблицею 5 легко підрахувати межі зміни доходу 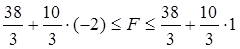 або
або 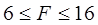 .
.
Обчислення інтервалів допустимих змін коефіцієнта с2* = 3 + d2 цільової функції (ринкова вартість кукурудзи), за умови, що вартість пшениці постійна с1 = 3 проводиться аналогічно. Пропонується це зробити самостійно.
Зауваження. Все попереднє обговорення стосувалося дослідження змін коефіцієнта при базисній змінній в результуючій симплекс-таблиці. Розглянемо тепер випадок, коли коефіцієнт при небазисній змінній S1 зміниться на d1 (0+d1S). В цьому випадку коефіцієнт при небазисній змінній S1 в результуючому F - рівнянні потрібно зменшити на ту саму величину, на яку він збільшується в початковому F - рівнянні. Оптимальне значення F при цьому, природньо, не зміниться.