Как определяются постоянные интегрирования в цепях первого порядка? Показать на конкретном примере.

Ответ: Постоянную интегрирования A определим на основании первого закона коммутации (3.1).Для момента времени t = 0 имеем 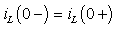, или .

Отсюда следует общая формула определения постоянной интегрирования для цепей первого порядка, включающих одну индуктивность:

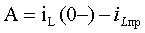
(3.13)

Для определения 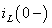нужно найти токи в цепи до коммутации (t= 0-). Исследуемая цепь представлена на рис. 3.5, в которой требуется определить ток i_L (0-). Снова решается задача расчета цепи постоянного тока, где индуктивность заменена короткозамкнутой перемычкой. Для решения могут быть использованы все методы расчета цепей постоянного тока, включая законы Кирхгофа и эквивалентные преобразования.

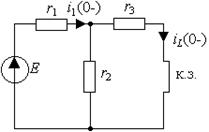
Рис. 3.5. Схема для анализа докоммутационного состояния цепи. Так как исследуемая цепь включает один источник энергии, то наиболее просто получить результат можно путем использования метода эквивалентных преобразований, вычисляя входное сопротивление цепи со стороны источника напряжения:

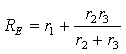
Тогда ток:

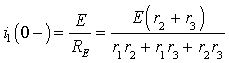
Искомый ток 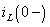является частью тока 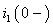и определяется правилом деления тока на части:

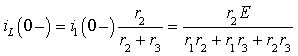
По формуле (3.13) окончательно определим постоянную интегрирования:

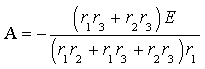
График функции тока 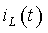схематично изображен на рис.3.6а. За время 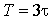ток почти приближается к установившемуся значению, и это время считается длительностью переходного процесса. Найденное выражение для переменной состояния позволяет определить все токи и напряжения. Для этого следует, опираясь на известную переменную состояния, решить обратную задачу: последовательно шаг за шагом, используя законы Ома и Кирхгофа, а также компонентные соотношения, определить токи и напряжения в других ветвях [1]. Для рассматриваемого примера найдем: а. Напряжение на индуктивности:

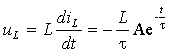
б. Ток:

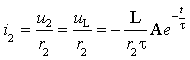
в. Ток:

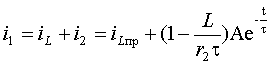
г. Напряжение:

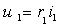
Все найденные как следствие функции имеют разрыв в точке t = 0.

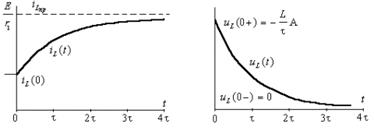
а) б)

Рис. 3.6. Графики переходного процесса: а)ток в индуктивности; б)напряжение на индуктивности

Например, график функции 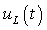, изображенный на рис.3.6б, претерпевает скачок от нулевого значения до уровня - L 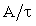(A - отрицательно), а затем плавно уменьшается до нулевого значения. Это означает, что, как правило, для функций, которые не являются переменными состояния, законы коммутации не выполняются, и, следовательно, определение для них постоянных интегрирования встречает дополнительные трудности. Если сразу искать выражения для этих функций, то требуется провести дополнительное исследование состояния цепи для момента времени t = 0+. Предложенный в этом пособии путь решения задачи через переменные состояния является наиболее оптимальным, так как требует знания только основных начальных условий, определяемых законами коммутации. Задача решена.