
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Изложить последовательность расчёта переходных процессов классическим методом. Показать на конкретном примере цепи первого порядка.
|
|
Ответ: Название метода «классический» отражает использование в нем решений дифференциальных уравнений с постоянными параметрами методами классической математики. Данный метод обладает физической наглядностью и удобен для расчета простых цепей (расчет сложных цепей упрощается операторным методом). Этапы расчета переходного процесса в цепи классическим методом: 1)Найти независимые начальные условия, то есть, напряжения на ёмкостях и токи на индуктивностях в момент начала переходного процесса. 2)Далее необходимо составить систему уравнений на основе законов Кирхгофа, Ома, электромагнитной индукции и т.д., описывающих состояние цепи после коммутации, и исключением переменных получить одно дифференциальное уравнение, в общем случае неоднородное относительно искомого тока 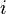 или напряжения
или напряжения 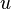 . Для простых цепей получается дифференциальное уравнение первого или второго порядка, в котором в качестве искомой величины выбирают либо ток в индуктивном элементе, либо напряжение на емкостном элементе. 3)Далее следует составить общее решение полученного неоднородного дифференциального уравнения цепи в виде суммы частного решения неоднородного дифференциального уравнения и общего решения соответствующего однородного дифференциального уравнения. 4)Наконец, в общем решении следует найти постоянные интегрирования из начальных условий, т. е. условий в цепи в начальный момент времени после коммутации. Применительно к электрическим цепям в качестве частного решения неоднородного дифференциального уравнения выбирают установившийся режим в рассматриваемой цепи (если он существует), т. е. постоянные токи и напряжения, если в цепи действуют источники постоянных ЭДС и токов, или синусоидальные напряжения и токи при действии источников синусоидальных ЭДС и токов. Токи и напряжения установившегося режима называют установившимися. Общее решение однородного дифференциального уравнения описывает процесс в цепи без источников ЭДС и тока, который поэтому называют свободным процессом. Токи и напряжения свободного процесса называют свободными, а их выражения должны содержать постоянные интегрирования, число которых равно порядку однородного уравнения.
. Для простых цепей получается дифференциальное уравнение первого или второго порядка, в котором в качестве искомой величины выбирают либо ток в индуктивном элементе, либо напряжение на емкостном элементе. 3)Далее следует составить общее решение полученного неоднородного дифференциального уравнения цепи в виде суммы частного решения неоднородного дифференциального уравнения и общего решения соответствующего однородного дифференциального уравнения. 4)Наконец, в общем решении следует найти постоянные интегрирования из начальных условий, т. е. условий в цепи в начальный момент времени после коммутации. Применительно к электрическим цепям в качестве частного решения неоднородного дифференциального уравнения выбирают установившийся режим в рассматриваемой цепи (если он существует), т. е. постоянные токи и напряжения, если в цепи действуют источники постоянных ЭДС и токов, или синусоидальные напряжения и токи при действии источников синусоидальных ЭДС и токов. Токи и напряжения установившегося режима называют установившимися. Общее решение однородного дифференциального уравнения описывает процесс в цепи без источников ЭДС и тока, который поэтому называют свободным процессом. Токи и напряжения свободного процесса называют свободными, а их выражения должны содержать постоянные интегрирования, число которых равно порядку однородного уравнения.