
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Понятие модели. Этапы процесса моделирования.
|
|
Объект – некоторая часть окружающего нас мира, которая может быть рассмотрена как единое целое.
Свойства объекта – совокупность признаков объекта, по которым его можно отличить от других объектов
Модель – это упрощенное представление о реальном объекте, процессе или явлении.
Моделирование – построение моделей для изучения объектов, процессов, явлений.
Модель – это такой материальный или мысленно представляемый объект, который в процессе исследования замещает объект-оригинал так, что его непосредственное изучение дает новые знания об объекте-оригинале. Метод моделирования основывается на принципе аналогии. Главная особенность моделирования в том, что это метод опосредованного познания с помощью объектов заместителей. Модель выступает как своеобразный инструмент познания, который исследователь ставит между собой и объектом и с помощью которого изучает интересующий его объект. Именно эта особенность метода моделирования определяет специфические формы использования абстракций, аналогий, гипотез, других категорий и методов познания.Важнейшим понятием при экономико-математическом моделировании является понятие адекватности модели, то есть соответствия модели моделируемому объекту или процессу. Адекватность модели в какой-то мере условное понятие, так как полного соответствия модели реальному объекту быть не может, что характерно для моделирования экономических систем. При моделировании имеется в виду и не просто адекватность, но соответствие по тем свойствам, которые считаются существенными для исследования.
Изучение одних сторон моделируемого объекта осуществляется ценой отказа от отражения других сторон. Поэтому любая модель замещает оригинал лишь в строго ограниченном смысле.
Модель воспроизводит изучаемый объект или процесс в упрощенном виде. Поэтому при построении любой модели перед исследователем всегда возникают две опасности: переупрощения и переусложнения. Отображая действительность, модель ее упрощает, отбрасывая все «второстепенное» и «побочное». Однако это упрощение не должно быть «произвольным» и грубым.
Процесс моделирования в общем может быть представлен в виде циклической схемы.
Все этапы определяются поставленной задачей и целями моделирования.
В процессе моделирования выделяют 4 этапа:
1. Постановка задачи.
• Описание задачи
Задача (или проблема) формулируется на обычном языке, и описание должно быть понятным. Главное на этом этапе – определить объект моделирования и понять, что собой должен представлять результат.
• Формулировка цели моделирования
Целями моделирования могут быть: познание окружающего мира, создание объектов с заданными свойствами («как сделать, чтобы…»), определение последствий воздействия на объект и принятие правильного решения («что будет, если…»), эффективность управления объектом (процессом) и т.д.
• Анализ объекта
На этом этапе, отталкиваясь от общей формулировки задачи, четко выделяют моделируемый объект и его основные свойства. Поскольку в большинстве случаев исходный объект – это целая совокупность более мелких составляющих, находящихся в некоторой взаимосвязи, то анализ объекта будет подразумевать разложение (расчленение) объекта с целью выявления составляющих и характера связей между ними.
2. Разработка модели (формализация задачи, связанная с созданием модели, то есть модели, записанной на каком-либо формальном языке).
В общем смысле формализация — это приведение существенных свойств и признаков объекта моделирования к выбранной форме.
Для решения задачи на компьютере больше всего подходит язык математики. В такой модели связь между исходными данными и конечными результатами фиксируется с помощью различных формул, а также накладываются ограничения на допустимые значения параметров.
• Информационная модель
На этом этапе выявляются свойства, состояния и другие характеристики элементарных объектов, формируется представление об элементарных объектах, составляющих исходный объект, т.е. информационная модель.
• Знаковая модель
Информационная модель, как правило, представляется в той или иной знаковой форме, которая может быть либо компьютерной, либо некомпьютерной.
• Компьютерная модель
Существует большое количество программных комплексов, которые позволяют проводить исследование (моделирование)информационных моделей. Каждая среда имеет свой инструментарий и позволяет работать с определенными видами информационных объектов, что обуславливает проблему выбора наиболее удобной и эффективной среды для решения поставленной задачи.
3. Компьютерный эксперимент
• План моделирования
План моделирования должен отражать последовательность работы с моделью. Первыми пунктами в таком плане должны стоять разработка теста и тестирование модели.
Тестирование – процесс проверки правильности модели.
Тест – набор исходных данных, для которых заранее известен результат.
В случае несовпадения тестовых значений необходимо искать и устранять причину.
• Технология моделирования
Технология моделирования – совокупность целенаправленных действий пользователя над компьютерной моделью.
4. Анализ результатов моделирования
Конечная цель моделирования – принятие решения, которое должно быть выработано на основе всестороннего анализа полученных результатов. Этот этап решающий – либо исследование продолжается (возврат на 2 или 3 этапы), либо заканчивается.
Основой для выработки решения служат результаты тестирования и экспериментов. Если результаты не соответствуют целям поставленной задачи, значит, допущены ошибки на предыдущих этапах. Это может быть слишком упрощенное построение информационной модели, либо неудачный выбор метода или среды моделирования, либо нарушение технологических приемов при построении модели. Если такие ошибки выявлены, то требуется редактирование модели, т.е. возврат к одному из предыдущих этапов. Процесс продолжается до тех пор, пока результаты моделирования не будут отвечать целям моделирования.
2. Управление как деятельность по принятию решений. Алгоритм процесса принятия решений: основные стадии и их характеристика.
Существует достаточно большое количество определений того, что есть управление, даваемых различными отраслями знания с учетом специфики той или иной из них. Только в менеджменте существует два основных подхода к определению того, что есть управление. В рамках функционального подхода – это совокупность функций по планированию, мотивации, организации и контролю, в рамках процессного подхода – это процесс, состоящий из ряда стадий: постановка цели, выбор исполнителей и средств, планирование путей ее достижения, организация ресурсов и исполнителей в рамках реализации плана, контроль за выполнением плана, анализ результатов деятельности по достижению цели.
Государственное управление – это деятельность по оказанию целенаправленного воздействия на различные сферы жизни человеческого общества, осуществляемая специальными уполномоченными на то общественными структурами – органами государственной власти и управления. Государство осуществляет управленческое воздействие на различные стороны жизнедеятельности общества.
Управленческое решение — это творческий акт субъекта управления, направленный на устранение проблем, которые возникли в объекте управления.
Принятие решений - это особый вид человеческой деятельности, направленный на выбор способа достижения поставленной цели. В широком смысле под решением понимают процесс выбора одного или нескольких вариантов действий из множества возможных.
Ни одна функция управления не может быть реализована иначе как посредством подготовки и исполнения управленческих решений. По существу, вся совокупность видов деятельности любого работника управления так или иначе связана с принятием и реализацией решений. Этим прежде всего определяется значимость деятельности по принятию решений и определению его роли в управлении.
Любое управленческое решение проходит три стадии. Рассмотрим их.
Первая стадия - уяснение проблемы - включает в себя: сбор информации; анализ информации; выяснение ее актуальности; определение условий, при которых проблема будет решена.
Вторая стадия - составление плана решения - включает в себя: разработку альтернативных вариантов решения; сопоставление их с имеющимися ресурсами; оценку альтернативных вариантов по социальным последствиям; оценку их по экономической эффективности; составление программ решения; разработку детального плана решения.
Третья стадия — выполнение решения — включает в себя доведение решений до конкретных исполнителей; разработку мер поощрений и наказаний; контроль за выполнением решений.
Работа менеджера над принятием решения состоит из ряда этапов:
- определение цели управления;
- диагностика проблемы;
- сбор информации, как основной, так и дополнительной;
- определение критериев ограничений;
- подготовка вариантов решений, в том числе альтернативных;
- оценка вариантов решений;
- выбор окончательного варианта.
Принятие решения является главным звеном в управлении — это творческий этап.
3. Поиск решения проблемы. Классификация проблем по степени структурированности.
Алгоритм принятия решений представляет собой шестифазовую последовательность.
В него входит не только собственно отыскание решения проблем (фаза 3), то есть анализ, анализ и выбор альтернатив на основе плановых и технико-экономических расчетов, но и выявление возникающих проблем (фаза1), а также постановка проблем (фаза 2), включая конструирования возможных действий подлежащих анализу. Опыт показывает, что две последние фазы процесса принятия решений (1 и 2), предшествующие оценки и выбору альтернатив, является, как правило, весьма сложными и ответственными, а зачастую и не менее трудно реализуемыми, их роль резко возрастает при переходе к решению нестандартных проблем, требующих творческого подхода к поиску решения. Не менее важное значение имеют в полном цикле решения проблем и последующие фазы – принятие решений уполномоченными на то руководителями (фаза 4), выполнение принятых решений (5.) и оценка результатов (6.). Обратная связь (от фазы 6 к фазе 3) стимулирует поиск новых решений, если результаты практического апробирования сделанного ранее выбора не приводят к решению выявленной проблемы. Строго говоря, обратная связь осуществляется в течении всего процесса принятия решений, взаимодействия управляющего и управляемого объектов.
Каждый класс проблем требует применения соответствующего метода нахождения решений, который в наибольшей степени будет способствовать выбору альтернативы, максимально приближающейся к оптимуму.
Укрупненная классификация методов нахождения решений базируется на понятии структуризации проблемы. Структура любой проблемы определяется пятью основными логическими элементами:
- цель или ряд целей, достижения которых будет означать, что проблема решена
- альтернативные средства, то есть курсы действий, с помощью которых может быть достигнута цель
- затраты ресурсов, требующихся для реализации каждого курса действий
- модель или модели, в которых с помощью некоторого формального языка (в том числе математики, формальной логики, обычного словесного, графического описания и т. п.) отображаются связи между целями, альтернативами и затратами
- критерий, с помощью которого сопоставляются в каждом конкретном случае цели и затраты и отыскивается наиболее предпочтительное решение.
Степень структуризации проблемы определяется тем, насколько хорошо выделены и осознаны указанные пять элементов проблемы. От этого зависит возможность применения для поиска решения того или иного метода.
Неструктурированные проблемы отличаются значительной неопределенностью и неформализуемостью как самих целей деятельности, так и возможных курсов действий (вариантов поведения). При решении этих проблем суждения, основанные на опыте, интуиции имеют весьма большое значение. Научные методы решения таких проблем состоят в использовании общих идей системного подхода в процессе систематизации мыслительной деятельности при рассмотрении проблем, а также в правильной организации экспертных опросов и квалифицированной обработке данных, получаемых на их основе.
К слабоструктурированным можно отнести такие проблемы, которые связаны с выработкой долгосрочных курсов действий, каждый из которых затрагивает многие аспекты деятельности отрасли или предприятия и реализуется поэтапно. Процесс решения этих проблем содержит наряду с хорошо изученными, количественно формализуемыми элементами также неизвестные и неизмеряемые компоненты, испытывающие сильное влияние фактора неопределенности.
Хорошо структурированные проблемы многовариантны по своему существу, но все их существенные элементы и связи могут быть выражены количественно. В этом случае наилучший из возможных вариантов решения может быть найден с помощью методов исследования операций и экономико-математического моделирования.
Стандартные проблемы, отличающиеся полной ясностью и однозначностью не только целей, альтернатив и затрат, но и самих вариантов решений, решаются на основе заранее выработанных процедур и правил. В частности, решение такой проблемы может быть однозначно получено на основе четко определенной методики.
Нужно подчеркнуть, что отнесение той или иной проблемы к одному из названных четырех классов не носит постоянного характера. В процессе все более глубокого изучения, анализа и осмысления проблемы она из неструктурированной может превратиться в структурированную (при повышении удельного веса формально-логического и математического описания в формулировке проблемы и ее элементов), затем в хорошо структурированную (полностью описываемую экономико-математической моделью), а в ряде случаев и в стандартную (сводимую к тривиальному, жестко алгоритмизированному процессу принятия решений или к выполнению рутинных, полностью автоматизированных операций).
Основным методом исследования систем, в том числе с целью решения проблем, возникающих при управлении ими, является моделирование. В случае с экономической системой часто требуется наличие комплексной модели экономики, охватывающей все аспекты ее функционирования и структуры. Экономико-математические методы и экономико-математические модели соотносятся между собой как инструменты и результат процесса моделирования.
По степени структурированности:
– слабоструктурированные (непрограммированные) принимаются в новых случаях; предполагают наличие недостоверной информации и большой выбор альтернатив; количество таких решений растет по мере роста масштабов организации
– высокоструктурированные (программируемые) являются результатом определенной последовательности шагов; ограничено число альтернатив; выбор происходит по заданной направленности в пределах правил и нормативов; принимаются на основе достоверной информации.
4. Классификация методов построения моделей (в частности, экономических) Понятие модели. Адекватность модели.
Моде́ ль — это упрощенное представление реального устройства и/или протекающих в нем процессов, явлений.
Построение и исследование моделей, то есть моделирование, облегчает изучение имеющихся в реальном устройстве свойств и закономерностей. Применяют для нужд познания.
Классификация:
· экономическая кибернетика: системный анализ, теория экономической информации и теория управляющих систем
· математическая статистика: экономические приложения данной дисциплины – выборочный метод, дисперсионный анализ, регрессионный анализ, многомерный статистический анализ, факторный анализ, теория индексов и др.
· математическая экономия и изучающая те же вопросы с количественной стороны эконометрия: теория экономического роста, теория производственных функций, межотраслевые балансы, национальные счета, анализ спроса и потребления, региональный и пространственный анализ, глобальное моделирование и др.
· методы принятия оптимальных решений, в том числе исследование операций в экономике: оптимальное программирование, в том числе методы ветвей и границ, сетевые методы планирования и управления, теория и методы управления запасами, теория массового обслуживания, теория игр, теория и методы принятия решений. В оптимальное программирование входят в свою очередь линейное программирование, нелинейное программирование, динамическое, дискретное, дробно-линейное, параметрическое, стохастическое, геометрическое программирование
· методы и дисциплины, специфичные отдельно как для централизованно планируемой экономики, так и для рыночной экономики. К первым можно отнести теорию системы оптимального функционирования экономики, оптимальное планирование, теорию оптимального ценообразования, модели материально-технического снабжения и др. Ко вторым – методы, позволяющие разработать модели свободной конкуренции, капиталистического цикла, модель монополии, индикативного планирования, модели теории фирм и т. д. Многие из методов, разработанных для централизованно планируемой экономики, могут оказаться полезными и при экономико-математическом моделировании в условиях рыночной экономики
· методы экспериментального изучения экономических явлений. К ним относятся, как правило, математические метолы анализа и планирования экспериментов экономического характера, методы машинной имитации, деловые игры. Сюда можно отнести также и методы экспертных оценок, разработанные для оценки явлений, с трудом поддающихся непосредственному измерению.
Метод моделирования основывается на принципе аналогии. Главная особенность моделирования в том, что это метод опосредованного познания с помощью объектов заместителей. Модель выступает как своеобразный инструмент познания, который исследователь ставит между собой и объектом и с помощью которого изучает интересующий его объект. Именно эта особенность метода моделирования определяет специфические формы использования абстракций, аналогий, гипотез, других категорий и методов познания. Качество модели зависит от ее способности отражать и воспроизводить предметы и явления объективного мира, их структуру и закономерный порядок.
Важнейшим понятием при экономико-математическом моделировании является понятие адекватности модели, то есть соответствия модели моделируемому объекту или процессу. Адекватность модели в какой-то мере условное понятие, так как полного соответствия модели реальному объекту быть не может, что характерно для моделирования экономических систем. При моделировании имеется в виду и не просто адекватность, но соответствие по тем свойствам, которые считаются существенными для исследования.
Построение модели предполагает наличие некоторых знаний об объекте-оригинале. Познавательные возможности модели обуславливается тем, что модель отображает какие-либо существенные черты объекта оригинала. Вопрос о необходимой и достаточной мере сходства оригинала и модели требует конкретного анализа. Очевидно, что модель утрачивает свой смысл как в случае тождества с оригиналом, так и в случае чрезмерного во всех существенных отношениях отличиях от оригинала.
Таким образом, изучение одних сторон моделируемого объекта осуществляется ценой отказа от отражения других сторон. Поэтому любая модель замещает оригинал лишь в строго ограниченном смысле. Из этого следует, что для одного объекта может быть постоянно несколько специализированных моделей, концентрирующих внимание на определенных сторонах исследуемого объекта или же характеризующих объект с разной степенью детализации.
Адекватность:
Адекватность модели — совпадение свойств (функций/параметров/характеристик и т. п.) модели и соответствующих свойств моделируемого объекта. Адекватностью называется совпадение модели моделируемой системы в отношении цели моделирования.
В процессе работы модель выступает в роли относительносамостоятельного квазиобъекта, позволяющего получить при исследовании некоторые знания о самом объекте. Если результаты такого исследования (моделирования) подтверждаются и могут служить основой для прогнозирования в исследуемых объектах, то говорят, что модель адекватна объекту. При этом адекватность модели зависит от цели моделирования и принятых критериев.
Проверка адекватности и корректировка модели. Проверка адекватности модели необходима, так как по неверным результатам моделирования могут быть приняты неверные решения. Проверка может производиться путем сравнения показателей, полученных на модели, с реальными, а также путем экспертного анализа. Желательно проведение такого анализа независимым экспертом. Если по результатам проверки адекватности выявляются недопустимые расхождения между системой и ее моделью, в модель вносят необходимые изменения.В общем случае под адекватностью понимают степень соответствия модели тому реальному явлению или объекту, для описания которого она строится.Вместе с тем, создаваемая модель ориентирована, как правило, на исследование определенного подмножества свойств этого объекта. Поэтому можно считать, что адекватность модели определяется степенью ее соответствия не столько реальному объекту, сколько целям исследования. В наибольшей степени это утверждение справедливо относительно моделей проектируемых систем (то есть в ситуациях, когда реальная система вообще не существует). Тем не менее, во многих случаях полезно иметь формальное подтверждение (или обоснование) адекватности разработанной модели. Один из наиболее распространенных способов такого обоснования — использование методов математической статистики. Суть этих методов заключается в проверке выдвинутой гипотезы (в данном случае — об адекватности модели) на основе некоторых статистических критериев.При проверке гипотез методами математической статистики необходимо иметь в виду, что статистические критерии не могут доказать ни одной гипотезы — они могут лишь указать на отсутствие опровержения.
Итак, каким же образом можно оценить адекватность разработанной модели реально существующей системы? Процедура оценки основана на сравнении измерений на реальной системе и результатов экспериментов на модели и может проводиться различными способами. Наиболее распространенные из них:
- по средним значениям откликов модели и системы;
- по дисперсиям отклонений откликов модели от среднего значения откликов системы;
- по максимальному значению относительных отклонений откликов модели от откликов системы.
5. Процесс создания модели. Схема цикла моделирования. Взаимосвязь этапов процесса моделирования
Процесс моделирования включает три элемента:
• субъект (исследователь),
• объект исследования,
• модель, определяющую (отражающую) отношения познающего субъекта и познаваемого объекта.
Первый этап построения модели предполагает наличие некоторых знаний об объекте-оригинале. Познавательные возможности модели обусловливаются тем, что модель отображает (воспроизводит, имитирует) какие-либо существенные черты объекта-оригинала. Вопрос о необходимой и достаточной мере сходства оригинала и модели требует конкретного анализа. Очевидно, модель утрачивает свой смысл как в случае тождества с оригиналом (тогда она перестает быть моделью), так и в случае чрезмерного во всех существенных отношениях отличия от оригинала. Таким образом, изучение одних сторон моделируемого объекта осуществляется ценой отказа от исследования других сторон. Поэтому любая модель замещает оригинал лишь в строго ограниченном смысле. Из этого следует, что для одного объекта может быть построено несколько «специализированных» моделей, концентрирующих внимание на определенных сторонах исследуемого объекта или же характеризующих объект с разной степенью детализации.
На втором этапе модель выступает как самостоятельный объект исследования. Одной из форм такого исследования является проведение «модельных» экспериментов, при которых сознательно изменяются условия функционирования модели и систематизируются данные о её «поведении». Конечным результатом этого этапа является множество (совокупность) знаний о модели.
На третьем этапе осуществляется перенос знаний с модели на оригинал — формирование множества знаний. Одновременно происходит переход с «языка» модели на «язык» оригинала. Процесс переноса знаний проводится по определенным правилам. Знания о модели должны быть скорректированы с учетом тех свойств объекта-оригинала, которые не нашли отражения или были изменены при построении модели.
Четвёртый этап — практическая проверка получаемых с помощью моделей знаний и их использование для построения обобщающей теории объекта, его преобразования или управления им.
Моделирование — циклический процесс. Это означает, что за первым четырёхэтапным циклом может последовать второй, третий и т. д. При этом знания об исследуемом объекте расширяются и уточняются, а исходная модель постепенно совершенствуется. Недостатки, обнаруженные после первого цикла моделирования, обусловленные малым знанием объекта или ошибками в построении модели, можно исправить в последующих циклах.
Сейчас трудно указать область человеческой деятельности, где не применялось бы моделирование. Разработаны, например, модели производства автомобилей, выращивания пшеницы, функционирования отдельных органов человека, жизнедеятельности Азовского моря, последствий атомной войны. В перспективе для каждой системы могут быть созданы свои модели, перед реализацией каждого технического или организационного проекта должно проводиться моделирование.
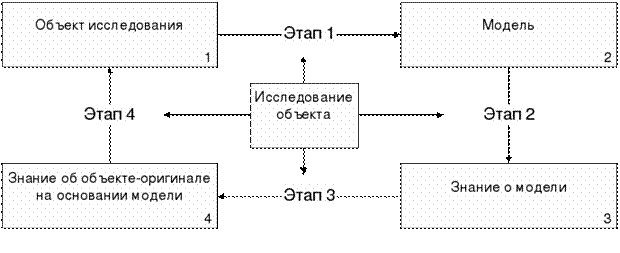
Взаимосвязи этапов. Вследствие того, что в процессе исследования обнаруживаются недостатки предшествующих этапов моделирования, между ними возникают возвратные связи. Уже на этапе построения модели может выясниться, что постановка задачи противоречива или приводит к слишком сложной математической модели. В соответствии с этим исходная постановка задачи корректируется. Далее математический анализ модели может показать, что небольшая модификация постановки задачи или ее формализация дает интересный аналитический результат.
Наиболее часто необходимость возврата к предшествующим этапам моделирования возникает при подготовке исходной информации. Может обнаружиться, что необходимая информация отсутствует или же затраты на ее подготовку слишком велики. Тогда приходится возвращаться к постановке задачи и ее формализации, изменяя их так, чтобы приспособиться к имеющейся информации.
Поскольку экономико-математические задачи могут быть сложны по своей структуре, иметь большую размерность, то часто случается, что известные алгоритмы и программы для ЭВМ не позволяют решить задачу в первоначальном виде. Если невозможно в короткий срок разработать новые алгоритмы и программы, исходную постановку задачи и модель упрощают: снимают и объединяют условия, уменьшают число факторов, нелинейные соотношения заменяют линейными, усиливают детерминизм модели и т. д.
Недостатки, которые не удается исправить на промежуточных этапах моделирования, устраняются в последующих циклах. Но результаты каждого цикла имеют и вполне самостоятельное значение. Начав исследование с построения простой модели, можно быстро получить полезные результаты, а затем перейти к созданию более совершенной модели, дополняемой новыми условиями, включающей уточненные математические зависимости.
По мере развития и усложнения экономико-математического моделирования его отдельные этапы обособляются в специализированные области исследований, усиливаются различия между теоретико-аналитическими и прикладными моделями, происходит дифференциация моделей по уровням абстракции и идеализации.
Теория математического анализа моделей экономики развилась в особую ветвь современной математики — математическую экономику. Модели, изучаемые в рамках математической экономики, теряют непосредственную связь с экономической реальностью — они имеют дело с исключительно идеализированными экономическими объектами и ситуациями. При построении таких моделей главным принципом является не столько приближение к реальности, сколько получение возможно большего числа аналитических результатов посредством математических доказательств. Ценность этих моделей для экономической теории и практики состоит в том, что они служат теоретической базой для моделей прикладного типа.
Довольно самостоятельными областями исследований становятся подготовка и обработка экономической информации и разработка математического обеспечения экономических задач (создание баз данных и бланков информации, программ автоматизированного построения моделей и программного сервиса для экономистов-пользователей). На этапе практического использования моделей ведущую роль должны играть специалисты в соответствующей области экономического анализа, планирования, управления.
Главным участком работы экономистов-математиков остается постановка и формализация экономических задач и синтезпроцесса экономико-математического моделирования.
6. Классификации видов моделей: в зависимости от исходного принципа построения; по общему целевому назначению; по степени агрегированности объектов моделирования; по цели создания и применения; по типу используемой информации; в зависимости от учета фактора времени; по типу используемого математического аппарата; по типу подхода к изучаемым явлениям.
Единой системы классификации экономико-математических моделей не существует. Для стратификации их на виды могут использоваться различные основания. Например, когда говорилось о понятии системы, виды моделей подразделялись на функциональные, структурные и информационные модели в зависимости от того, какое описание системы положено в основу модели.
По общему целевому назначению модели делятся на теоретико-аналитические, используемые при изучении общих свойств и закономерностей процессов, и прикладные, применяемые в целях решения конкретных задач управления: анализа, прогнозирования и планирования.
По степени агрегирования объектов моделирования модели экономических систем разделяются на макроэкономические и микроэкономические. Хотя четко разграничения между ними нет, к первым принято относить модели, отражающие функционирование экономики как единого целого, в то время как ко вторым относят модели отдельных фирм, предприятий, организаций.
По конкретному предназначению, то есть по цели создания и применения, можно выделить:
1) балансовые модели, выражающие требование соответствия наличия ресурсов и их использования;
2) трендовые модели, в которых развитие моделируемой системы отражается через тренд ее основных показателей; (тренд в экономике — направление преимущественного движения показателей.)
3) оптимизационные модели, предназначенные для осуществления выбора наилучшего варианта из ограниченного множества возможных;
4) имитационные модели, предназначенные для использования в процессе машинной имитации изучаемых систем или процессов и др.
По типу информации, используемой в моделях, они делятся на аналитические, построенные на априорной информации, и идентифицируемые, построенные на апостериорной информации.
По учету фактора неопределенности модели можно разделить на детерминированные, если в них результаты на выходе однозначно определяются управляющими воздействиями, и стохастические (вероятностные), если при задании на входе модели определенной совокупности значений на ее выходе могут получаться различные результаты в зависимости от действия случайного фактора.
По учету фактора времени модели подразделяются на статические модели, описывающие состояние системы в определенный момент времени (единовременный срез информации по данному объекту). Примеры моделей: классификация животных…., строение молекул, список посаженных деревьев, отчет об обследовании состояния зубов в школе и тд.; и динамические, модели, описывающие процессы изменения и развития системы (изменения объекта во времени). Примеры: описание движения тел, развития организмов, процесс химических реакций.
Математические модели могут классифицироваться также по характеристике математических объектов, включенных в модель, по типу математического аппарата, используемого в модели. По этому признаку могут быть выделены матричные модели, модели линейного и нелинейного программирования, корреляционно-регрессионные модели, модели теории игр, модели сетевого планирования и управления и т. д.
По типу подхода к изучаемым социально-экономическим системам можно подразделить модели на дескриптивные и нормативные. Дескриптивный подход в моделировании предполагает создание модели, предназначенной для описания и объяснения фактически наблюдаемых явлений и/или для прогноза этих явлений. Трендовые модели – яркий пример именно дескриптивных моделей. При нормативном подходе исследователя, управленца интересует не столько то, каким образом устроена и как развивается система, а то, как она должна быть устроена и как должна функционировать в смысле выполнения определенных критериев. Оптимизационные модели, например, по смыслу относятся к нормативным моделям.
По целям исследований
В зависимости от целей исследования выделяют следующие модели:
• функциональные. Предназначены для изучения особенностей работы (функционирования) системы, её назначения во взаимосвязи с внутренними и внешними элементами;
• функционально-физические. Предназначены для изучения физических (реальных) явлений, используемых для реализации заложенных в систему функций;
• модели процессов и явлений, такие как кинематические, прочностные, динамические и другие. Предназначены для исследования тех или иных свойств и характеристик системы, обеспечивающих её эффективное функционирование.
по общему назначению
• Технические
• Экономические
• Социальные и т.д.
7. Общее понятие эконометрических моделей. Виды эконометрических моделей. (дополнительно есть в тетради т.1 вопр.2)
Эконометрические модели – это формализованное описание различных экономических явлений и процессов.Эконометрические модели являются составляющими более широкого класса ЭММ. Данная модель выступает в качестве средств анализа и прогнозирования конкретных экономических процессов, как на макро, так и на микро уровнях на основе реальной статистики.
Эконометрическая модель, учитывая корреляционные связи, позволяет путем подбора аналитической зависимости построить модель на базисном периоде и при достаточной адекватности модели использовать ее для краткосрочного прогноза.
Виды эконометрических моделей:
• парная регрессия (устанавливает зависимость между двумя переменными);
• множественная регрессия (переменная зависит от двух или более факторов);
• система экономических уравнений (факторы от которых зависит переменная требуют не одного, а нескольких уравнений);
• модели временных рядов (значение переменной за ряд последовательных моментов времени).
Экономические переменные, участвующие в любой эконометрической модели (например y=f(x)), делятся на четыре вида:
• экзогенные (независимые) — переменные, значения которых задаются извне. В определенной степени данные переменные являются управляемыми (x);
• эндогенные (зависимые) — переменные, значения которых определяются внутри модели, или взаимозависимые (y);
• лаговые — экзогенные или эндогенные переменные в эконометрической модели, относящиеся к предыдущим моментам времени и находящиеся в уравнении с переменными, относящимися к текущему моменту времени. Например, xi-1 — лаговая экзогенная переменная, yi-1 — лаговая эндогенная переменная;
• предопределенные (объясняющие переменные) — лаговые (xi-1) и текущие (x) экзогенные переменные, а также лаговые эндогенные переменные (yi-1).
Тот же вопрос про виды, но подробно:
Главным инструментом эконометрического исследования является модель. Выделяют три основных класса эконометрических моделей:
1. модель временных рядов;
2. модели регрессии с одним уравнением;
3. системы одновременных уравнений.
Моделью временных рядов называется зависимость результативной переменной от переменной времени или переменных, относящихся к другим моментам времени.
К моделям временных рядов, характеризующих зависимость результативной переменной от времени, относятся:
а) модель зависимости результативной переменной от трендовой компоненты или модель тренда;
б) модель зависимости результативной переменной от сезонной компоненты или модель сезонности;
в) модель зависимости результативной переменной от трендовой и сезонной компонент или модель тренда и сезонности.
К моделям временных рядов, характеризующих зависимость результативной переменной от переменных, датированных другими моментами времени, относятся:
а) модели с распределённым лагом, объясняющие вариацию результативной переменной в зависимости от предыдущих значений факторных переменных;
б) модели авторегрессии, объясняющие вариацию результативной переменной в зависимости от предыдущих значений результативных переменных;
в) модели ожидания, объясняющие вариацию результативной переменной в зависимости от будущих значений факторных или результативных переменных.
Кроме рассмотренной классификации, модели временных рядов делятся на модели, построенные по стационарным и нестационарным временным рядам.
Стационарным временным рядом называется временной ряд, который характеризуется постоянными во времени средней, дисперсией и автокорреляцией, т. е. данный временной ряд не содержит трендовой и сезонной компонент.
Нестационарным временным рядом называется временной ряд, который содержит трендовую и сезонную компоненты.
Моделью регрессии с одним уравнением называется зависимость результативной переменной, обозначаемой как у, от факторных (независимых) переменных, обозначаемых как х1, х2, …, хn. Данную зависимость можно представить в виде функции регрессии или модели регрессии:
y=f(x, β)=f(х1, х2, …, хn, β 1…β k)
где β 1…β k – параметры модели регрессии.
Можно выделить две основных классификации моделей регрессии::
а) классификация моделей регрессии на парные и множественные регрессии в зависимости от числа факторных переменных;
б) классификация моделей регрессии на линейные и нелинейные регрессии в зависимости от вида функции f(x, β).
В качестве примеров моделей регрессии с одним уравнением можно привести следующие модели:
а) производственная функция вида Q=f(L, K), выражающая зависимость объёма производства определённого товара (Q) от производственных факторов – от затрат капитала (К) и затрат труда (L);
б) функция цены Р=f(Q, Pk), характеризующая зависимость цены определённого товара (Р) от объема поставки (Q) и от цен конкурирующих товаров (Pk);
в) функция спроса Qd=f(P, Pk, I), характеризующая зависимость величины спроса на определённый товар (Р) от цены данного товара (Р), от цен товаров-конкурентов (Pk) и от реальных доходов потребителей (I).
Системой одновременных уравнений называется модель, которая описывается системами взаимозависимых регрессионных уравнений.
Системы одновременных уравнений могут включать в себя тождества и регрессионные уравнения, в каждое из которых могут входить не только факторные переменные, но и результативные переменные из других уравнений системы.
Регрессионные уравнения, входящие в систему одновременных уравнений, называются поведенческими уравнениями. В поведенческих уравнениях значения параметров являются неизвестными и подлежат оцениванию.
Основное отличие тождеств от регрессионных уравнений заключается в том, что их вид и значения параметров известны заранее.
Примером системы одновременных уравнений является модель спроса и предложения, в которую входит три уравнения:
а) уравнение предложения: =а0+а1*Рt+a2*Pt-1;
б) уравнение спроса: =b0+b1* Рt+b2*It;
в) тождество равновесия: QSt = Qdt,
где QSt – предложение товара в момент времени t;
Qdt – спрос на товар в момент времени t;
Рt – цена товара в момент времени t;
Pt-1 – цена товара в предшествующий момент времени (t-1);
It – доход потребителей в момент времени.
В модели спроса и предложения выражаются две результативные переменные:
а) Qt – объём спроса, равный объёму предложения в момент времени t;
б) Pt – цена товара в момент времени t.
8. Процесс построения эконометрической модели. (6 вопрос из статистики)
Выделяют семь основных этапов эконометрического моделирования:
1) постановочный этап, в процессе осуществления которого определяются конечные цели и задачи исследования, а также совокупность включённых в модель факторных и результативных экономических переменных. При этом включение в эконометрическую модель той или иной переменной должно быть теоретически обоснованно и не должно быть слишком большим. Между факторными переменными не должно быть функциональной или тесной корреляционной связи, потому что это приводит к наличию в модели мультиколлинеарности и негативно сказывается на результатах всего процесса моделирования;
2) априорный этап, в процессе осуществления которого проводится теоретический анализ сущности исследуемого процесса, а также формирование и формализация известной до начала моделирования (априорной) информации и исходных допущений, касающихся в частности природы исходных статистических данных и случайных остаточных составляющих в виде ряда гипотез;
3) этап параметризации (моделирования), в процессе осуществления которого выбирается общий вид модели и определяется состав и формы входящих в неё связей, т. е. происходит непосредственно моделирование.
К основным задачам этапа параметризации относятся:
а) выбор наиболее оптимальной функции зависимости результативной переменной от факторных переменных. При возникновении ситуации выбора между нелинейной и линейной функциями зависимости, предпочтение всегда отдаётся линейной функции, как наиболее простой и надёжной;
б) задача спецификации модели, в которую входят такие подзадачи, как аппроксимация математической формой выявленных связей и соотношений между переменными, определение результативных и факторных переменных, формулировка исходных предпосылок и ограничений модели.
4) информационный этап - сбор необходимой статистической информации, т.е. регистрация значений участвующих в модели факторов и показателей; а также анализ качества собранной информации;
5) этап идентификации модели, в ходе осуществления которого происходит статистический анализ модели и оцененивание неизвестных параметров. Данный этап непосредственно связан с проблемой идентифицируемости модели, т. е. ответа на вопрос «Возможно ли восстановить значения неизвестных параметров модели по имеющимся исходным данным в соответствии с решением, принятым на этапе параметризации». После положительного ответа на этот вопрос решается проблема идентификации модели, т. е. реализуется математически корректная процедура оценивания неизвестных параметров модели по имеющимся исходным данным;
6) этап оценки качества модели, в ходе осуществления которого проверяется достоверность и адекватность модели, т. е. определяется, насколько успешно решены задачи спецификации и идентификации модели, какова точность расчётов, полученных на её основе. Построенная модель должна быть адекватна реальному экономическому процессу. Если качество модели является неудовлетворительным, то происходит возврат ко второму этапу моделирования;
7) этап интерпретации результатов моделирования.
К наиболее распространённым эконометрическим моделям относятся:
1. модели потребительского и сберегательного потребления;
2. модели взаимосвязи риска и доходности ценных бумаг;
3. модели предложения труда;
4. макроэкономические модели (модель роста);
5. модели инвестиций;
6. маркетинговые модели;
7. модели валютных курсов и валютных кризисов и др.
Эконометрическое исследование связано с решением следующих проблем:
1. качественный анализ связей экономических переменных, т. е. определение зависимых (yi) и независимых (хi) переменных;
2. изучение соответствующего раздела экономической теории;
3. подбор данных;
4. спецификация формы связи между yi и хi;
5. оценка неизвестных параметров модели;
6. проверка ряда гипотез о свойствах распределения вероятностей для случайной компоненты (гипотезы о средней дисперсии и ковариации);
7. анализ мультиколлинеарности объясняющих переменных, оценка ее статистической значимости, определение переменных, ответственных за мультиколлинеарность;
8. введение фиктивных переменных;
9. выявление автокорреляции;
10. выявление тренда, циклической и случайной компонент;
11. проверка остатков модели на гетероскедастичность;
12. анализ структуры связей и построения системы одновременных уравнений;
13. проверка условия идентификации;
14. оценка параметров системы одновременных уравнений;
15. проблемы моделирования на основе системы временных рядов;
16. построение рекурсивных моделей, авторегрессионных моделей;
17. выработка управленческих решений
18. прогноз экономических показателей, характеризующих изучаемый процесс;
19. моделирование поведения процесса при различных значениях независимых (факторных) переменных.