
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Построение системы показателей. Принципы отбора факторов модели. Построение многофакторных моделей. Отбор факторов.
|
|
Построение моделей множественной регрессии включает несколько этапов:
1) Выбор формы связи (уравнения регрессии).
2) Отбор факторных признаков.
Требования к включаемым факторам:
-количественно измеримы;
-не должны находиться в точной функциональной связи или быть сильно коррелированы.
2 этапа отбора факторов:
– исходя из сущности проблемы;
– на основе корреляционной матрицы и t- статистики параметров регрессии
Чем ближе к 1 определитель матрицы межфакторной корреляции, тем меньше мультиколлинеарность факторов
3) Обеспечение достаточного объема совокупности.
Важным этапом построения уже выбранного уравнения множественной регрессии является отбор и последующее включение факторных признаков.
С одной стороны, чем больше факторных признаков включено в уравнение, тем оно лучше описывает явление. Однако модель размерностью 100 и более факторных признаков сложно реализуема и требует больших затрат машинного времени. Сокращение размерности модели за счет исключения второстепенных, экономически и статистически несущественных факторов способствует простоте и качеству ее реализации. В то же время построение модели регрессии малой размерности может привести к тому, что такая модель будет недостаточно адекватна исследуемым явлениям и процессам.
Проблема отбора факторных признаков для построения моделей взаимосвязи может быть решена на основе интуитивно-логических или многомерных математико-статистических методов анализа.
Наиболее приемлемым способом отбора факторных признаков является шаговая регрессия (шаговый регрессионный анализ). Сущность метода шаговой регрессии заключается в реализации алгоритмов последовательного " включения", " исключения" или " включения-исключения" факторов в уравнение регрессии и последующей проверке их статистической значимости. Наиболее широкое применение получили следующие методы построения уравнения множественной регрессии:
1. Метод исключения – отсев факторов из полного его набора.
2. Метод включения – дополнительное введение фактора.
3. Шаговый регрессионный анализ – исключение ранее введенного фактора.
10. Методы отбора факторов: метод включения и исключения.
Важной составляющей процесса построения эконометрической модели является отбор факторов, существенно влияющих на изучаемый показатель и подлежащих включению в разрабатываемую модель. Оптимальный набор факторов определяется на основе качественного и количественного анализа. Прежде всего, на этапе постановки задачи и содержательного экономического анализа экономической модели отбираются факторы, влияние которых должно быть учтено при построении модели. В ряде случаев набор факторов определяется однозначно или с большой степенью уверенности. Например, спрос на товар определяется в основном ценой и доходом.
В более сложных случаях на следующем этапе с помощью формальных статистических методов проверяется целесообразность включения в модель каждого фактора.
Прежде всего, факторы проверяются на наличие тесной линейной корреляционной зависимости между ними. Признаком наличия линейной корреляционной зависимости между факторами xi и xj является условие
rxixj ≥ r1кр.
где rxi x j - выборочный линейный коэффициент корреляции, определяемый соотношением
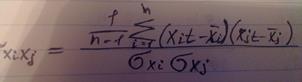
n-количество наблюдений, r1кр-критическое значение r1кр≈ 0, 8-0, 9 (определяется эмпирически).
Существование тесной корреляционной зависимости между факторами приводит к получению ненадежных оценок параметров модели.
Для преодоления сильной межфакторной корреляции применяется ряд подходов:
– исключение из модели одного или нескольких факторов. Из двух коррелирующих факторов исключаются тот, который более коррелирует с остальными факторами;
– преобразование факторов, при котором уменьшается корреляция между ними. Например, переходят от исходных переменных к их линейным комбинациям, не коррелированным друг с другом (метод главных компонент). При построении модели на основе рядов динамики переходят от первоначальных данных к первым разностям уровней ряда ∆ yt=yt-yt-1, чтобы исключить влияние тенденции.
Одним из критериев включения факторов в модель является степень их изолированного влияния на результативный признак, определяемая с помощью коэффициента парной корреляции ryxi. Отбираются факторы xi, удовлетворяющие условию rxixj ≥ r2кр
где r 2 кр ≈ 0, 5-0, 6 (определяется эмпирически).При определении «оптимального» набора факторов могут использоваться два метода:
1. Метод исключения – отсев факторов из полного его набора.
2. Метод включения – дополнительное введение фактора.
Согласно методу включения, сначала строится уравнение регрессии с одним наиболее влияющим фактором (фактор, для которого значение парного коэффициента корреляции с результативным признаком ryxi больше по модулю). Затем в него последовательно вводятся следующие факторы и определяется пара наиболее влияющих факторов. На следующем к первым двум добавляется еще по одному фактору и определяется наилучшая тройка факторов и т. д. На каждом шаге строится модель регрессии и проверяется значимость факторов. В модель включают только значимые факторы. Для проверки значимости фактора могут использоваться либо критерий Стьюдента, либо частный критерий Фишера. Процесс заканчивается, когда не остается факторов, которые следует включить в модель.
Согласно методу исключения сначала строится уравнение регрессии с полным набором факторов, из числа которых затем последовательно исключаются незначимые (наименее значимые) факторы. На каждом шаге исключается только один фактор, так как после исключения какого-либо фактора другой фактор, бывший до этого незначимым, может стать значимым. Процесс заканчивается, когда не остается факторов, которые следует исключить из модели.
Методы включения и исключения не гарантируют определение оптимального набора факторов, но в большинстве случаев дают результаты либо оптимальные, либо близкие к ним.
Не рекомендуется включать в модель очень большое число факторов, так как это может затруднить выявление качественных закономерностей и возрастает опасность включения в модель несущественных случайных факторов.
Кроме того, для получения достаточно надежных оценок параметров желательно, чтобы количество наблюдений превышало количество определяемых параметров не менее чем в 6-7 раз.