Методы нахождения точек условного экстремума.

Лекция № 11

Условный экстремум

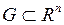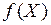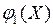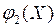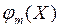
Пусть на открытом множестве заданы функции , , , 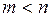. Обозначим 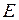– множество точек, координаты которых удовлетворяют уравнениям:

, , . (*)

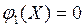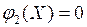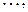
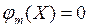Уравнения (*) называют ограничениями или уравнениями связи.

Определение. Точка 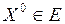называется точкой условного строгого максимума, если 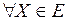выполняется неравенство .

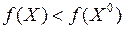Если 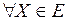выполняется неравенство 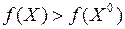, то точку 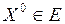называют точкой условного строгого минимума.

Методы нахождения точек условного экстремума.

1. Метод исключения. Рассмотрим уравнения связи 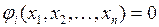, 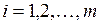. Если уравнения связи удается разрешить относительно каких-то 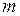переменных: 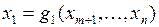, , 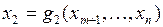, , 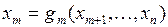то исследование функции на условный экстремум сводится к исследованию на обычный экстремум функции 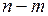переменных.

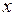Пример 1. Найти экстремум функции при условии, что и 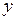удовлетворяют уравнению связи .

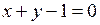Решение. Разрешим уравнение связи относительно переменной 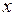: 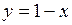. Подставив выражение для 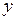в функцию, получим 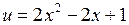. Исследуем на экстремум функцию одной переменной.

, .

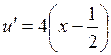Следовательно, 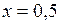точка минимума функции. Исходная функция в точке 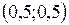имеет условный минимум.

Пример 2. Найти условные экстремумы функции 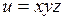относительно уравнений связи , .

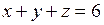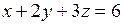Решение. Разрешим уравнения связи относительно переменных 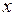и : , .

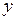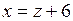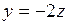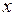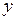Подставив найденные значения и в выражения для 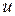, сведем задачу к исследованию на обычный (безусловный) экстремум функции 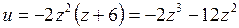. . 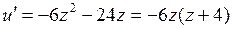Стационарные точки 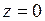и .

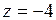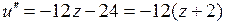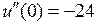, , . Следовательно, в точке 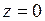функция имеет максимум 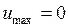, а в точке 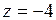– минимум .

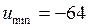Исходная функция при заданных ограничениях имеет один условный максимум 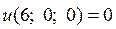и один условный минимум .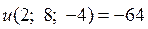