Достаточные условия существования условного экстремума.

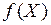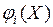
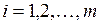Пусть и дважды непрерывно дифференцируемы в окрестности точки 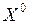, в которой выполняются необходимые условия существования условного экстремума функции 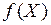при ограничениях .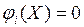

Если при выполнении условий

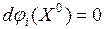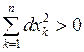, (1)

второй дифференциал 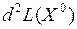является положительно (отрицательно) определенной квадратичной формой, то функция 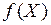в точке 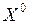имеет условный минимум (максимум).

Если при условиях (1) 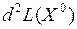является неопределенной квадратичной формой, то в точке 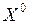условного экстремума нет.

Пример 3. Найти экстремум функции 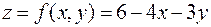при условии, что переменные 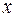и 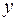удовлетворяют уравнению .

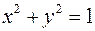Пример 4. Найти условный экстремум функции

относительно уравнения связи .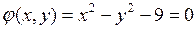

Решение. Функци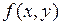и и 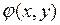дважды непрерывно дифференцируемы. Матрица Якоби , .

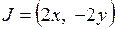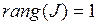Строим функцию Лагранжа .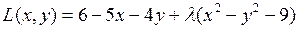

Необходимые условия:

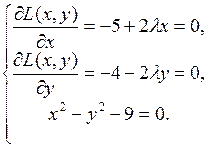
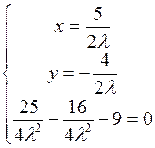
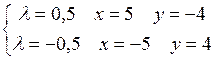
В точках 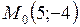и 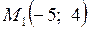может быть условный экстремум.

Достаточные условия:

, , . , .

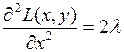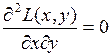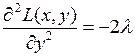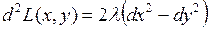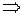
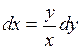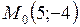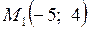
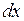В точках и и 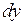связаны соотношением 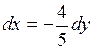, поэтому 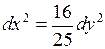и .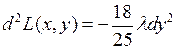

Точке 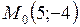соответствует 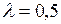поэтому 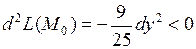и в точке 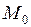условный максимум.

Точке 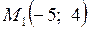соответствует 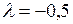поэтому 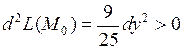и в точке 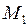условный минимум.