Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Способы расчета
|
|
В качестве исходных данных для расчетов, берутся данные Δ q или T.
Для расчета первой горизонтальной производной по дискретным значениям наблюденного поля пользуются одной из формул (по выбору): (1), (3), (7).
При этом вторые производные можно рассчитать либо по специальным формулам (2), (4), (5), (8), либо по формулам первой производной, но уже по графику рассчитанной первой производной, т.е. либо
U —> Uxx, либо U -> Ux —> Uxx
При расчетах Ux и Uxx важно правильно оценить размерности и единицы измерения рассчитываемых величин.
Физический смысл – скорость возрастания или убывания функции
Геометрический смысл 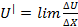
Область применения – Для интерпретации гравимагнитных аномалий
Сущность и необходимость - для выделения локальных аномалий
6. Аналитическое продолжение исходного поля. Сущность и необходимость аналитического продолжения.
Аналитические продолжения - процедуры по нахождению значений поля в любой точке пространства вне участка плоскости (линии) наблюдения. Как правило, это делается по дискретным значениям наблюденного поля. В зависимости от целевой направленности трансформации проблема аналитического продолжения распадается на несколько проблем:
аналитическое продолжение в верхнюю полуплоскость или аналитическое продолжение в верхнее полупространство: Рассмотрим один из самых доступных. Если гармоническая функция задана на линии (профиля наблюдения), то задача ее определения во внешней области решается интегралом Пуассона. Для любой точки верхней полуплоскости Р (x1-h)
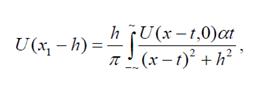
где h - высота пересчета, х - абсцисса точки, в которой рассчитывают поле, t - переменная по участку сканирования. В этом случае удобно центр участка сканирования совмещать с началом координат (x=0), тогда:
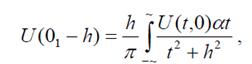
Отсюда следует, что значение поля в некоторой точке верхней полуплоскости (на высоте h) является интегральным средним наблюденного поля в пределах угла видимости φ является исходной для построения различных палеток (Андреева, Логачева). Для построения палетки из точки P(01i-h), для которой определяют аналитически продолженное значение поля U(01-h), проводят пучок лучей (в сторону профиля наблюдения) через равные углы видимости:
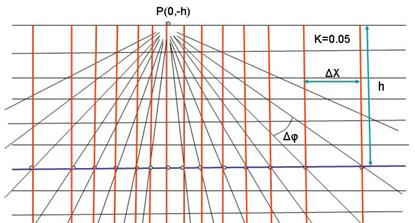
Расчетное значение поля на высоте h в точке P(01i-h) будет равно
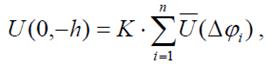
K – постоянный коэффициент, зависящий от способа разбиения лучами.
Точность расчетов будет тем больше, чем меньше Δ φ, и чем длиннее профиль и интервал палетки по оси x.
аналитическое продолжение в нижнюю полуплоскость или аналитическое продолжение в нижнее полупространство: Из всех рассматриваемых видов трансформаций аналитическое продолжение в нижнюю полуплоскость (нижнее полупространство) является наиболее важным. Широко известно высказывание на этот счет американского геофизика СИ. Пирсона о том, что пересчеты наблюденных полей на более низкие горизонты можно уподобить фокусирующей линзе, приближающей изучаемый объект к исследователю. Задача о продолжении потенциальных функций в сторону возмущающих масс относится к некорректно поставленным. Это означает, что даже при малых погрешностях в исходных данных расчетные значения поля на любых уровнях ниже поверхности наблюдения могут значительно отличаться от истинных значений в этих точках. Особенно велики погрешности расчетных значений вблизи возмущающего объекта (особых точек).
Способов пересчета вниз много. Наиболее простые из них метод сеток, метод Рейнбоу, метод, основанный на разложении исходной функции в ряд Тейлора, и др. В настоящее время чаще других применяются палетки В.Н. Страхова, Г.И. Каратаева, формулы А.К. Маловичко, С.В. Шалаева, К.Е. Веселова и М.У. Сагитова и др. Наиболее часто при аналитическом продолжении прибегают к непосредственному пересчету, основанному на решении интеграла Пуассона:
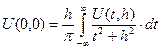
Наиболее удобные рабочие формулы, выведенные Шалаевым, Каратаевым и др.
С.В. Шалаев 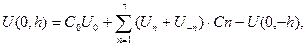
Г.А. Каратаев 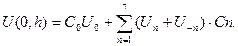
Так же для расчетов приводятся сопутствующие абсциссы узлов и коэффициентов!!!!!
Область применения – Для интерпретации гравимагнитных аномалий
Сущность и необходимость - для выделения локальных аномалий
7. Преобразование Фурье. Спектры и их свойства
Под преобразованием Фурье понимается разложение сигнала по периодическим функциям синусов и косинусов. Спектр – это функция, описывающая распределение амплитуд и фаз по различным частотным составляющим (гармоникам) сигнала, начиная с низкочастотных и кончая высокочастотными составляющими. Суммирование частотных составляющих с учетом их амплитуд и фаз приводит к восстановлению формы сигнала.
Практическое применение анализа Фурье при обработке геофизических данных связано с их представлением в виде сигналов, заданных в дискретных точках наблюдений, т.е.
S (Х= r∆)= Sr или S(t= r∆ t)= Sr.
Построение спектров дискретно заданного сигнала основано на теореме о том,
что любую непрерывную периодическую функцию, удовлетворяющую условиям
Дирихле (функция ограничена и имеет конечное число разрывов, т.е. любые
геофизические данные удовлетворяют этим условиям) можно представить в виде
конечного ряда Фурье:
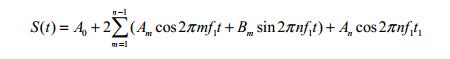
содержащего n-констант Am и Bm, называемых коэффициентами Фурье и
определяемых таким образом, чтобы значения непрерывного S(t) и дискретного Sr
сигналов совпадали бы в точках t=r∆, т.е. S(r∆)=Sr.
Выражения для коэффициентов Фурье:
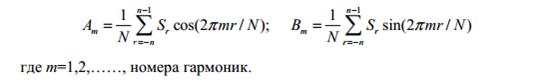
По коэффициентам Фурье рассчитываются спектры дискретно заданного сигнала:
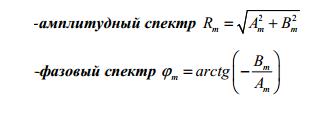
Амплитудный спектр описывает распределение амплитуд по различным частотам. Фазовый спектр показывает отклонение фазы определенной частоты относительно начала отсчета.
По амплитудному и фазовому спектрам можно получить выражение для комплексного спектра:
-комплексный спектр Sm представляет комплексное число:
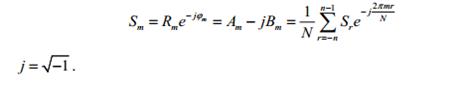 :
:
Известно, что для комплексного числа имеется комплексно-сопряженное, определяющее
-комплексно-сопряженный спектр Sm∗ :
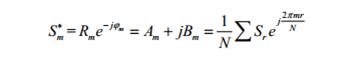
Комплексно-сопряженный спектр представляет зеркальное отображение комплексного спектра в область отрицательных гармоник. Кроме перечисленных видов спектров часто используется энергетический спектр;
-энергетический спектр есть произведение комплексного спектра на комплексно-сопряженный или квадрат амплитудного спектра, т.е. Sm⋅ Sm∗ = Rm2.
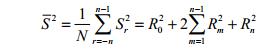
Вычисление спектров представляет прямое преобразование Фурье. Вычисление значений сигнала по его спектрам представляет обратное преобразование Фурье


8. Оценка частотного состава поля (частотные характеристики поля).
Частотной характеристикой трансформации (преобразования) принято называть отношение спектра трансформационной функции к спектру исходной (нетрансформированной):
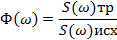
Все частотные трансформации используют частотные характеристики смещения.
Для того чтобы получить частотные характеристику дискретной трансформации – нужно проделать трансформации с частотными характеристиками смещения.
Пример: