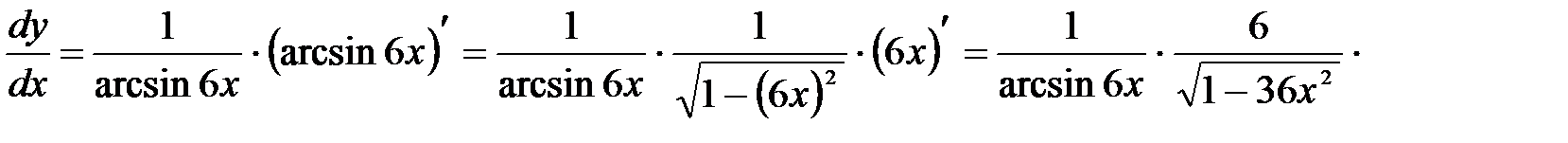Задача 1. Примеры решения задач

Примеры решения задач

Найти указанные пределы:

1) ; ; 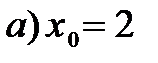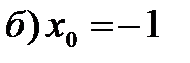b)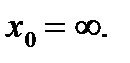

2) ;

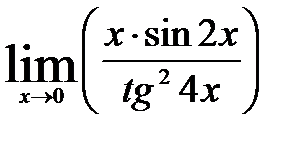3) ;

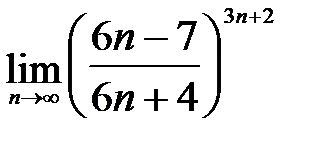4)

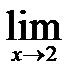
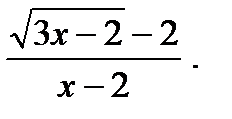
а) При подстановке вместо переменной 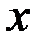ее предельного значения 2 получаем

= =

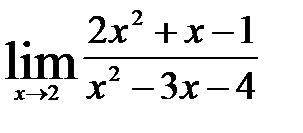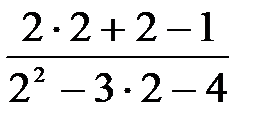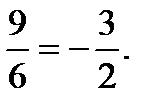
б) При подстановке вместо переменной 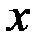ее предельного значения -1 получается неопределенность вида .

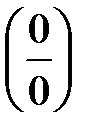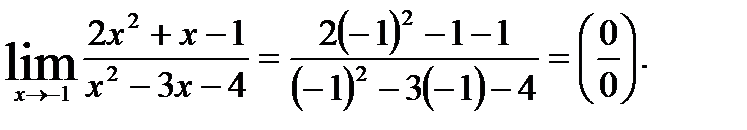Для избавления от этого типа неопределенности в нашем случае представим квадратные трехчлены числителя и знаменателя в виде произведения линейных множителей, воспользовавшись известной формулой:

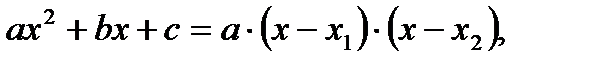где 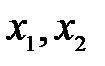- корни квадратного трехчлена

.

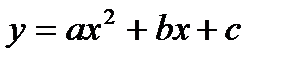У нас 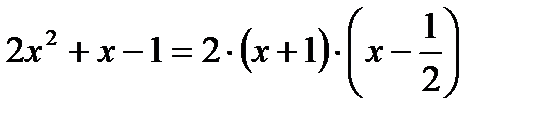, так как дискриминант квадратного трехчлена

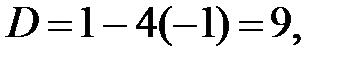следовательно, .

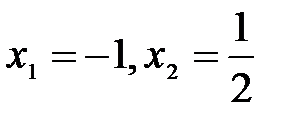Аналогично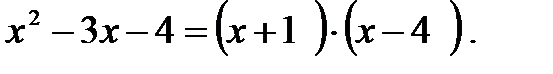

Теперь условие примера можно переписать в другом виде и продолжить решение:

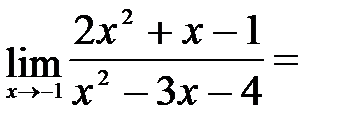
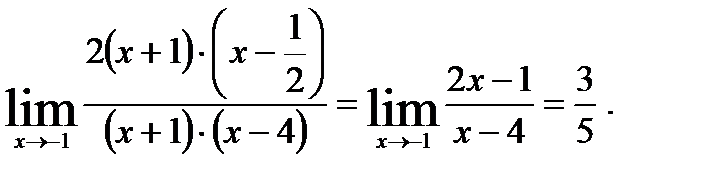
b)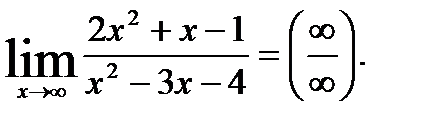

Здесь сталкиваемся с неопределенностью 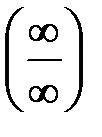, избавиться от которой можно вынесением за скобки в числителе и знаменателе дроби старшей степени переменной или предварительно числитель и знаменатель данной дроби разделить на 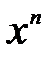, где n- наивысшая степень числителя и знаменателя.

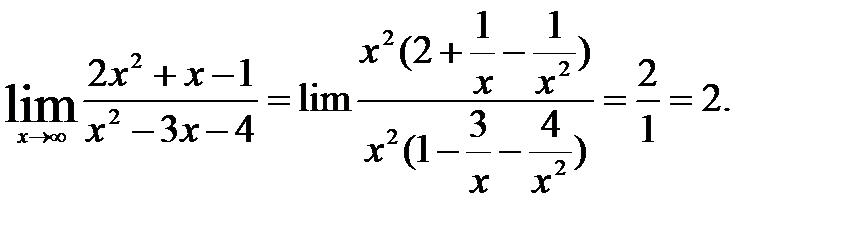
Найти пределы:

2)

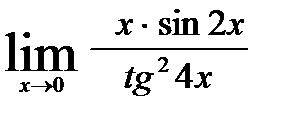
3)

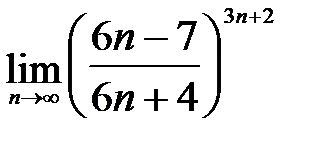
В первом случае для освобождения от неопределенности будем использовать первый замечательный предел и одно из очевидных следствий:

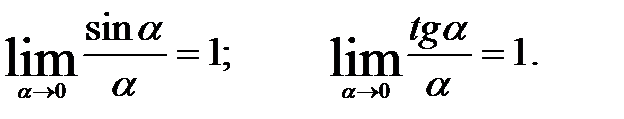
Решение примера будет выглядеть следующим образом:

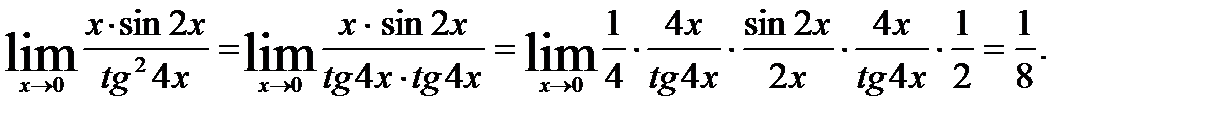
Во втором случае для освобождения от неопределенности будем использовать второй замечательный предел и одно из очевидных следствий:

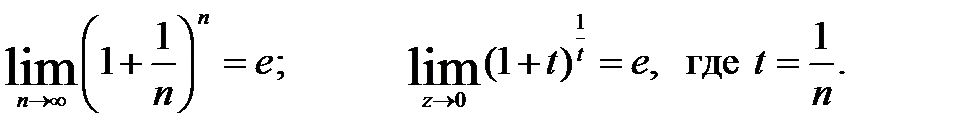
Решение примера будет выглядеть следующим образом:

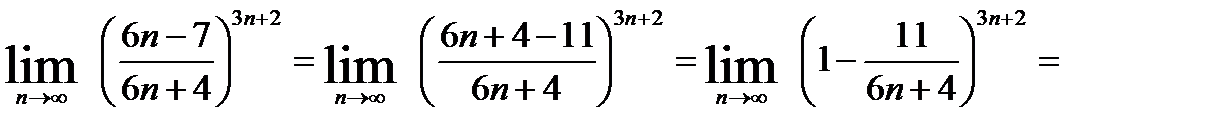
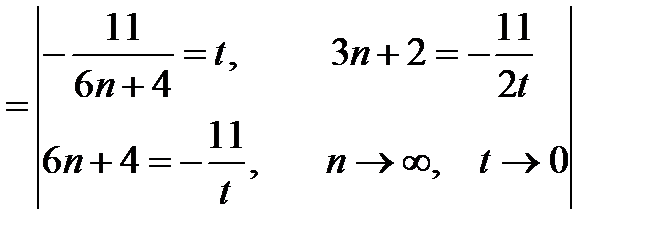
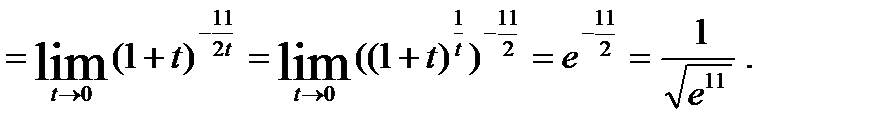
Вычислить:

4)

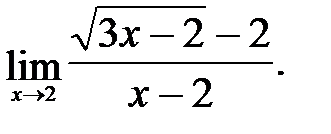
Непосредственная подстановка предельного значения аргумента 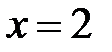приводит к неопределенности вида 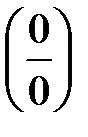. Чтобы раскрыть эту неопределенность, умножим числитель и знаменатель дроби на сумму

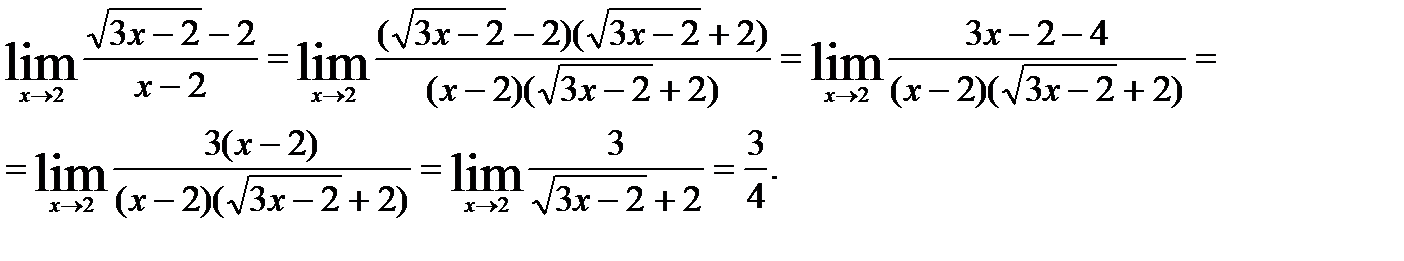
Задача 2.

Найти производные 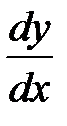, пользуясь правилами и формулами дифференцирования. При решении всех последующих примеров кроме таблицы производных будут использованы известные правила дифференцирования суммы, разности, произведения, дроби и теорема о производной сложной функции.

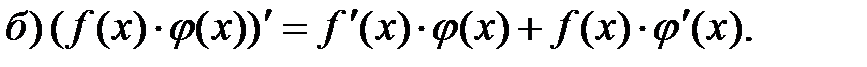
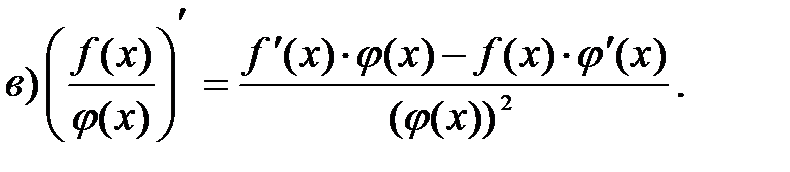
г) Если задана сложная функция 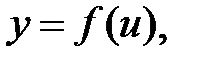где 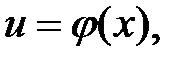то есть 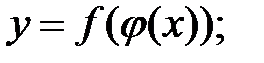если каждая из функций 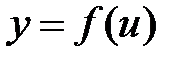и дифференцируема по своему аргументу, то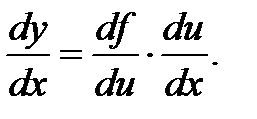

1)

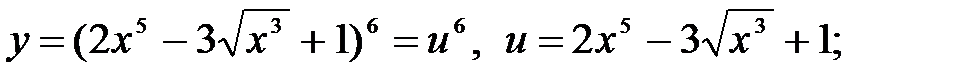
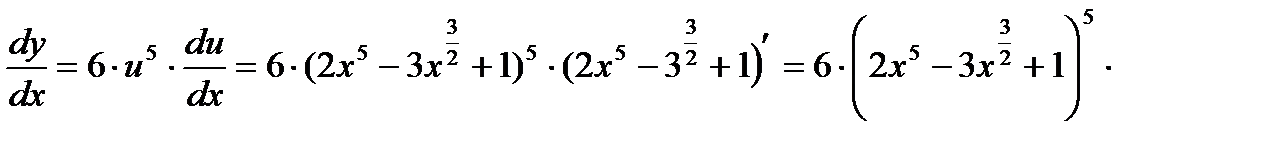
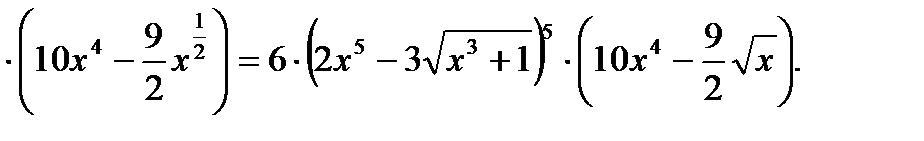
2)

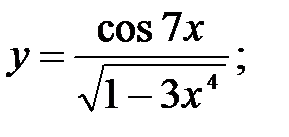
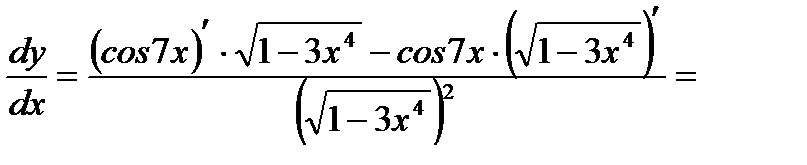
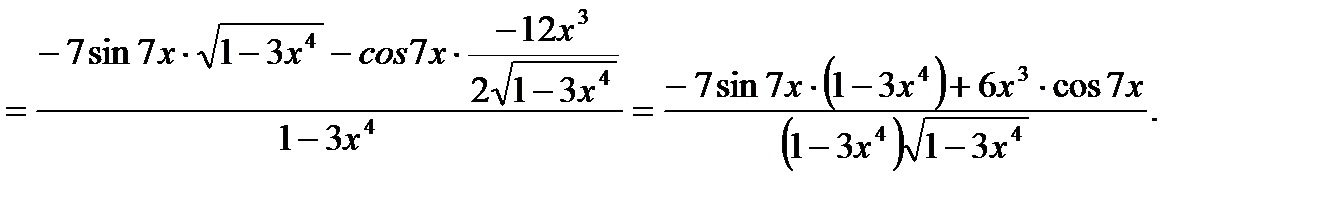
3)

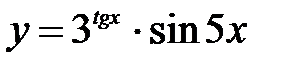
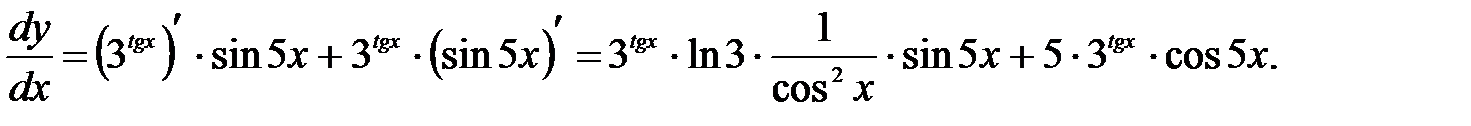
4) ;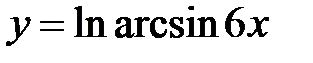