Простые и сложные проценты

ПРАКТИКУМ

ПО ФИНАНСОВОЙ МАТЕМАТИКЕ

(автор Галиаскаров Ф.М.)

Глава 1. Основные формулы, применяемые в финансовых расчетах

Простые и сложные проценты

Под процентной ставкой понимается относительная величина дохода за фиксированный отрезок времени.

Проценты различаются по базе их начисления. Применяется постоянная или последовательно изменяющаяся база для расчета. В последнем случае за базу применяется сумма, полученная на предыдущем этапе наращения или дисконтирования, т.е. проценты начисляются на проценты. При постоянной базе используют простые, при измененной - сложные процентные ставки.

Под наращенной суммой ссуды (долга, депозита, других видов выданных в долг или инвестированных денег) понимают первоначальную ее сумму с начисленными процентами к концу срока.

Наращение по простой процентной ставке:

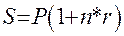, (1)

где S – наращенная сумма; P – первоначальная сумма, n – срок, r – ставка наращения (десятичная дробь).

Наращение по сложной процентной ставке:

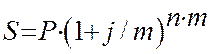, (2)

где j - сложная процентная ставка; n - число лет наращения, m – число начислений процентов в году.

Номинальная ставка – это годовая ставка сложных процентов при одноразовом начислении процентов в году по ставке j.

Эффективная ставка – это годовая ставка сложных процентов, которая дает тот же результат, что и m-разовое начисление процентов в году по ставке .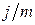

Наращение по непрерывной процентной ставке:

При непрерывном наращении процентов применяют особый вид процентной ставки - силу роста (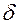). Сила роста характеризует относительный прирост наращенной суммы за бесконечно малый промежуток времени. Она может быть постоянной или изменяться во времени.

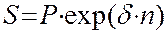, (3)

Дисконтирование и учет по простым процентным ставкам.

Термин дисконтирование употребляется как средство определения любой стоимостной величины, относящейся к будущему, на некоторый, более ранний момент времени.

В финансовой практике часто сталкиваются с задачей, обратной наращению процентов: по заданной сумме S, которую следует уплатить через некоторое время n, необходимо определить сумму полученной ссуды P. Такая ситуация может возникнуть, например при разработке условий контракта. Расчет P по S необходим и тогда, когда проценты с суммы S удерживаются вперед, т.е. непосредственно при выдаче ссуды. В этом случае говорят, что сумма S дисконтируется или учитывается, сам процесс начисления процентов и их удержание называется учетом, а удержанные проценты - дисконтом

В зависимости от вида процентной ставки применяют два метода дисконтирования - математическое дисконтирование и банковский (коммерческий) учет. В первом случае используется ставка наращения, во втором - учетная ставка.

Математическое дисконтирование представляет собой формальное решение задачи, обратной наращению первоначальной суммы ссуды.

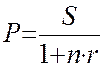, (4)

Банк или иное финансовое учреждение до наступления срока платежа по векселю или иному платежному обязательству приобретает его у владельца по цене, которая меньше суммы, указанной на векселе, т.е. покупает (учитывает) его с дисконтом (т.е. со скидкой). Получив при наступлении срока векселя деньги, банк реализует дисконт. При учете векселя применяется банковский или коммерческий учет, согласно этому методу проценты за пользование ссудой в виде дисконта начисляются на сумму, подлежащую уплате в конце срока. При этом применяется учетная ставка d.

, (5)

Для ставки наращения прямой задачей является определение наращенной суммы, обратной – дисконтирование. Для учетной ставки, наоборот, прямая задача заключается в дисконтировании, обратная – в наращении.

Ставка Прямая задача Обратная задача

r 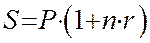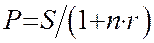(6)

d .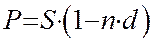

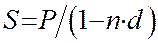Учетная ставка отражает фактор времени более жестко. Например, при d = 20 % уже 5-ти летний срок достаточен для того, чтобы владелец векселя ничего не получил при его учете.

Определение срока ссуды и величины простой процентной ставки

Продолжительность срока ссуды в годах получим, решив уравнения (1) и (5) относительно n:

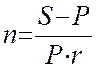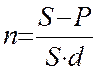, (7) , (8)

По этим же уравнениям можно определить и процентные ставки:

, (9) 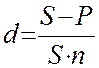, (10)

Определение срока платежа и сложных процентных ставок.

Продолжительность срока платежа в годах получим, решив уравнения (2) относительно n:

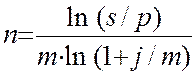, (11)

Поэтому же уравнению можно определить и сложную процентную ставку:

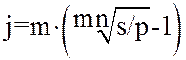, (12)

Продолжительность срока платежа в годах при наращении по постоянной силе роста 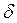и по изменяющейся с постоянным темпом силе роста получим, решив уравнения (3) относительно n:

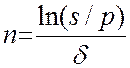, (13)

Поэтому же уравнению можно определить и силе роста :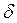

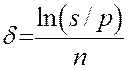, (14)

1.2. Потоки платежей. Постоянные финансовые ренты

Погашение задолженности в рассрочку, периодическое поступление доходов от инвестиций, выплата пенсий и т.д. – называют потоки платежей.

Потоки платежей могут быть регулярными и нерегулярными. В нерегулярном потоке платежей членами являются как положительные (поступления), так и отрицательные величины (выплаты), а соответствующие платежи могут производиться через разные интервалы времени.

Поток платежей, все члены которого положительные величины, а временные интервалы между платежами одинаковы, называют финансовой рентой или просто рентой.

Рента характеризуется следующими параметрами: член ренты - размер отдельного платежа, период ренты – временной интервал между двумя последовательными платежами, срок ренты – время от начала первого периода ренты до конца последнего периода, процентная ставка.

По количеству выплат членов ренты на протяжении года, ренты делятся на годовые, P - срочные (P – количество выплат в году), непрерывные (много раз в году).

Обобщенные параметры потоков платежей

Анализ потока платежей предполагает расчет одной из двух обобщающих характеристик: наращенной суммы или современной стоимости.

Наращенная сумма –сумма всех членов потока платежей с начисленными на них к концу срока процентами.

Современная стоимость потока платежей – сумма всех его членов, дисконтированных на начало срока ренты или некоторый упреждающий момент времени.

Допустим, имеется ряд платежей 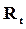, выплачиваемых спустя время 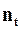после некоторого начального момента времени, общий срок выплат n лет. Необходимо определить наращенную на конец срока сумму потока платежей, если проценты начисляются раз в году по сложной ставке j, то:

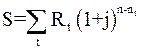, (15)

Как видим, наращенную сумму в заданных условиях получают методом прямого счета. Современную стоимость такого потока найдем прямым счетом – как сумму дисконтированных платежей. Обозначив эту величину, как A, получим:

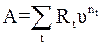, (16)

где 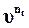- дисконтный множитель по ставке j.

Между величинами A и S существует функциональная зависимость:

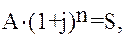(17)

Очень важным является различие рент по моменту выплат платежей в пределах периода. Если платежи осуществляются в конце периодов, то такие ренты называют обыкновенными или постнумерандо, если же платежи производятся в начале периодов, то их называют пренумерандо.

Годовая рента

В течении n лет в банк в конце каждого года вносится по R руб. На взносы начисляются сложные проценты по ставке % годовых. Все члены ренты, кроме последнего, приносят проценты – на первый член ренты начисляются (n-1) раз, на второй (n-2) и т.д.

.

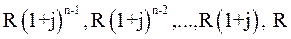Если переписать этот ряд в обратном порядке, то получим геометрическую прогрессию со знаменателем (1+ j) и первым членом R.

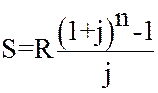, (18)

При начислении процентов m раз в году то:

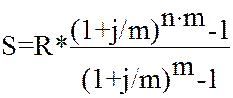; (19)

Если платежи осуществляются в начале периодов то

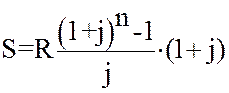; (20)

При начислении процентов m раз в году то:

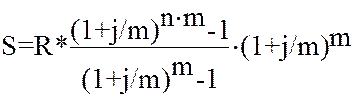; (21)

Современная стоимость постоянной ренты постнумерандо

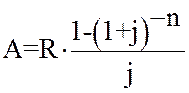, (22)

Множитель, на который умножается R, называется коэффициентом приведения ренты и обозначается :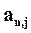

При 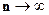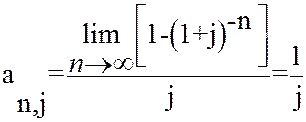, (23)

В этом случае: 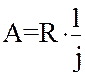, (24)

При дисконтировании m раз в году:

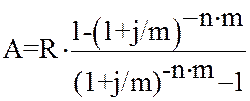, (25)

Определение срока ренты

P=1

m=1

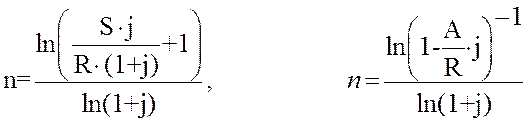
p=1

m> 1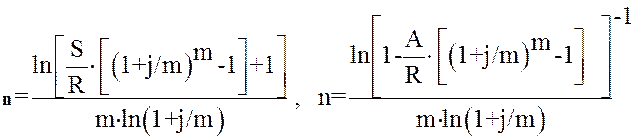

P> 1

m=1

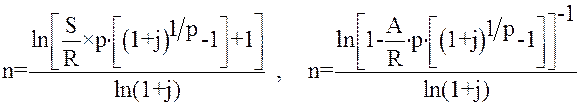
m=p

m¹ p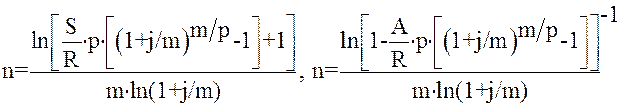

При расчете срока ренты необходимо принять во внимание следующие моменты:

1. Расчетные значения срока будут дробные. Для годовой ренты в качестве n удобнее принять меньшее ближайшее число. У p-срочной ренты результат округляется до ближайшего целого числа периодов.

2. Если округление производится до меньшего целого числа, то наращенная сумма или современная стоимость ренты оказывается меньше заданной. Возникает необходимость в соответствующей компенсации. Например, если речь идет о погашении задолженности путем выплаты постоянной ренты, то компенсация может быть осуществлена соответствующими платежом в начале или конце срока или с повышением суммы члена ренты.