Двойные интегралы.

1.1. Определение двойного интеграла

Рассмотрим в плоскости Oxy замкнутую область (D), ограниченную линией (L). Пусть в области (D) задана непрерывная функция 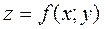^. Разобьём область произвольными линиями на n частей (D₁), (D₂),.. (D_n), которые будем называть площадками или элементарными областями. Символами 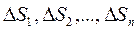будем обозначать площади соответствующих площадок.

В каждой из площадок выберем произвольную точку 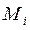(рис. 1).

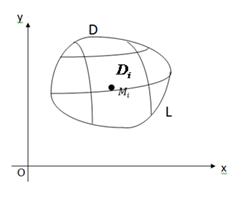
Рис. 1

Тогда получим n точек 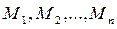. Обозначим через 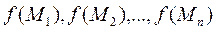значения функции в выбранных точках и составим сумму произведений:

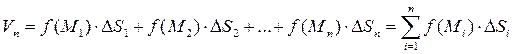
Сумма 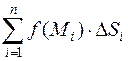называется интегральной суммой для функции 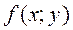в области (D).

Диаметром замкнутой ограниченной поверхности называется наибольшее расстояние между точками её границы.

Обозначим через λ наибольший из диаметров элементарных областей (D₁), (D₂),.. (D_n): 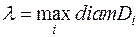, где .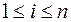

Если существует предел интегральной суммы 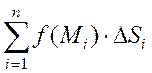, при λ → 0 (n→ ∞), не зависящий ни от способа разбиения области (D) на элементарные области 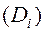, ни от выбора точек в каждой элементарной области, то этот предел называют двойным интегралом от функции 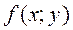по области (D) и обозначают:

.

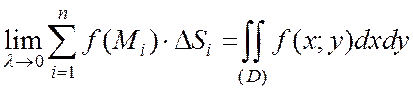При этом функция 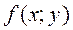называется подынтегральной функцией;

dS – элементом площади, (D) – областью интегрирования.

Двойной интеграл может обозначаться и так:

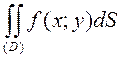
1.2. Геометрический смысл двойного интеграла.

Пусть дана функция 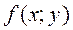, непрерывная и неотрицательная в области (D). Найдём объём тела, ограниченного сверху поверхностью 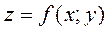, снизу областью (D) и с боков – прямой цилиндрической поверхностью, направляющей которой служит замкнутый контур, ограничивающий область (D) (рис. 2).

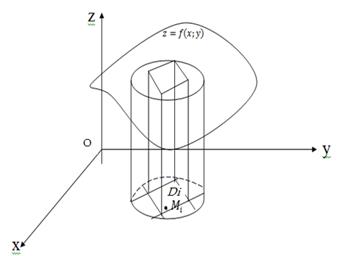
Рис. 2

Для нахождения объёма V данного цилиндра разобьём область (D) произвольным образом на n элементарных областей без общих внутренних точек, площади которых обозначим через .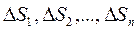

В каждой из этих элементарных областей выберем произвольную точку 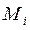и построим прямой цилиндрический столбик с основанием 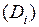и высотой 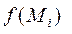. Объём такого столбика равен . Сумма объёмов этих цилиндрических столбиков представляет собой объём ступенчатого тела, приближённо заменяющего объём данного цилиндра. Эта сумма будет тем точнее выражать искомый объём V, чем меньше будет λ (наибольший из диаметров элементарных областей):

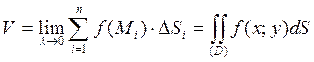
Итак, двойной интеграл с неотрицательной подынтегральной функцией выражает объём соответствующего тела:

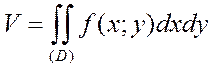
1.3. Свойства двойных интегралов

1)Двойной интеграл от суммы интегрируемых в области (D) функци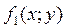й и 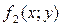равен сумме двойных интегралов от этих функций:

2) Постоянный множитель можно вынести за знак двойного интеграла:

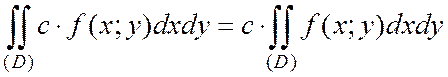, (с =const)

3) Если область (D) разбита на две области (D ₁) и (D ₂) без общих внутренних точек и функция интегрируема в области (D), то

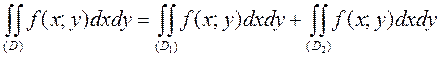
4) Если во всех точках области (D) выполняется неравенство 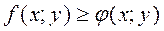и функции и 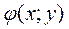интегрируемы в области (D), то

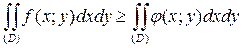
5)Если m и M – соответственно наименьшее и наибольшее значения интегрируемой в области (D) функции 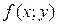, S – площадь области (D), то значение двойного интеграла заключено между произведениями наименьшего и наибольшего значений подынтегральной функции на площадь области интегрирования:

6) Если 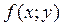— интегрируемая в области (D) функция, то

7) (Теорема о среднем)

Двойной интеграл равен произведению значения подынтегральной функции в некоторой точке 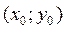области интегрирования на площадь области интегрирования S (при условии, что функция 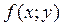непрерывна в замкнутой области (D)):

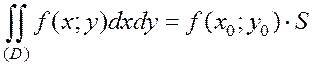
1.4. Вычисление двойных интегралов

Рассмотри область (D), ограниченную линиями ,

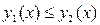(), x=a, x=b (a< b), где 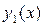и 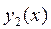непрерывны на [a; b] (рис. 3)

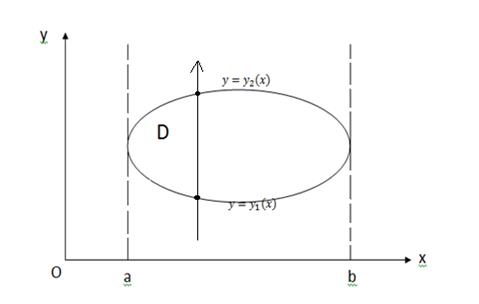
Рис. 3

Каждая из кривых 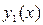и 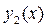пересекаются любой прямой, параллельной оси Oy, в одной точке (область называют правильной относительно оси Oy).

Выражение

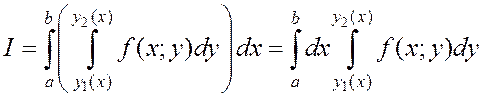
называют двукратным интегралом по области (D). Интеграл в правой части называют повторным.

Замечание.

При вычислении двойного интеграла сначала вычисляют внутренний интеграл по переменной y, считая x постоянным. Затем внешний интеграл по переменной x.

Если же область (D) ограничена «слева» линией 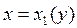, «справа» – линией 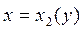, снизу – прямой y=c, сверху – прямой y=d, причём каждая из кривых 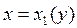и 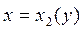пересекаются любой прямой, параллельной оси Oх, в одной точке.

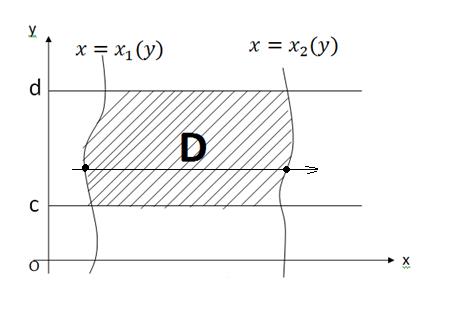
Рис. 4

Тогда

.

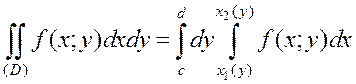Замечание. При вычислении двойного интеграла сначала вычисляют внутренний интеграл по переменной x, считая у постоянным. Затем внешний интеграл по переменной у.

Теорема. Если область разбита на две подобласт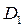и () и (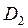) прямой, параллельной оси Ox или оси Oy, причём любая прямая, параллельная оси Ox или оси Oy, пересекает границу област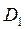и () и (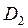) не более чем в двух точках, то двукратный интеграл по области (D) равен сумме таких же интегралов по областям (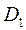) и ():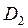

.

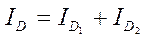Замечания.

1.При вычислении двойного интеграла следует помнить, что внутренний интеграл берётся от линии до линии, внешний от точки до точки.

2.Если внешний интеграл вычисляется по x, то пределы внутреннего интеграла функции от x (в частном случае константы). Если внешний интеграл вычисляется по у, то пределы внутреннего интеграла функции от у (в частном случае константы).

Пример

Найти пределы интегрирования двукратного интеграла 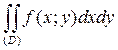, если область (D) ограничена линиями: y=x, y=2x, y=6-x.

Решение

Построим область (D) (рис. 5).

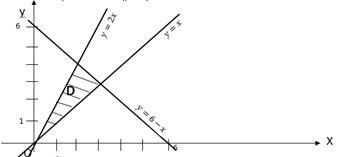
Рис. 5

Если будем проводить прямые, параллельные оси Oy, то «сверху» эти прямые будут пересекать границу области (D) по двум линиям: y=2x и y=6-x. Аналогично будет и в случае, если пересекать область (D) линиями, параллельными оси Ox.

Поэтому в точке пересечения линий y=2x и y=6-x (при x=2) проведём линию, параллельную оси Oy, тем самым разбив область (D) на две подобласт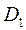и () и (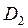) (рис. 6).

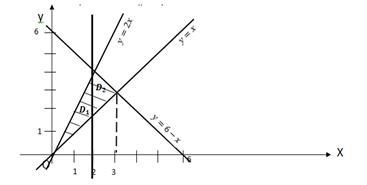
Рис. 6

Тогда

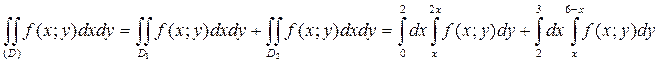1.5. Двойной интеграл в полярных координатах.

Рассмотрим двойной интеграл 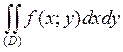. Введём полярную систему координат .

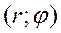Известно, что .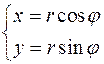

При переходе к полярной системе координат элемент площади равен 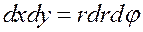, r -якобиан перехода. Пусть область (D^*) ограничена лучами, образующими с полярной осью углы 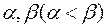и кривыми .

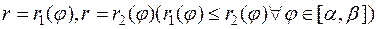Пусть в полярной системе координат каждый луч пересекает границу области (D^*) не более чем в двух точках (рис. 7).

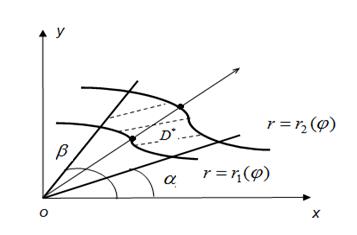
Рис. 7

Тогда имеет место формула

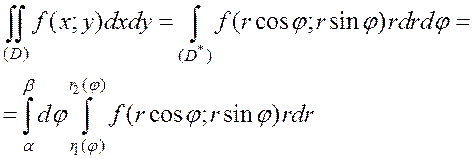
Замечание. Переход к полярным координатам целесообразен, если областью интегрирования является круг или сектор или если подынтегральная функция содержит выражение вида .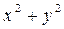

Пример

Вычислить

,

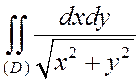где (D) – часть круга с центром в начале координат и радиусом 1, расположенная во второй четверти.

Решение

Изобразим область (рис. 8).

Рис. 14

Рис.8

Для вычисления интеграла используем формулу перехода к полярным координатам. При этом

,
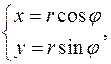
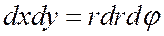
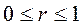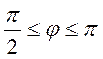
Тогда