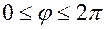Геометрические приложения двойного интеграла.

2.1. Вычисление объёма.

Объём тела, ограниченного сверху поверхностью 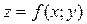, где 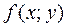– неотрицательная функция, плоскостью z=0 и цилиндрической поверхностью с основанием (D), равен двойному интегралу от функции 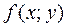по области (D):

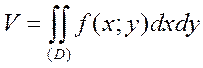
Пример

Найти объём тела, ограниченного поверхностями x=0, y=0, z=0, x+y+z=1.

Решение

Изобразим область (D).

x=0, y=0, z=0 – координатные плоскости; x+y+z=1 или z=1-x-y – плоскость, проходящая через точки (1; 0; 0), (0; 1; 0), (0; 0; 1) (рис. 9).

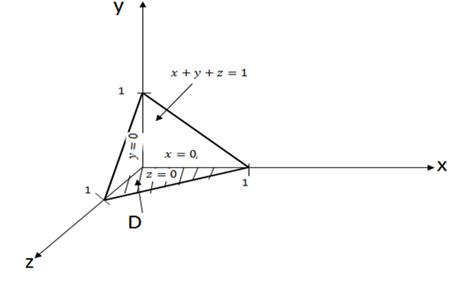
Рис. 9

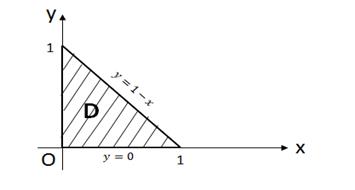Проекцией полученной пирамиды на плоскость Oxy является область (D). Изобразим её в системе координат Oxy (рис. 10).

Рис. 10

Область (D): x=0, y=0, y=1-x. Тогда, используя формулу вычисления объема при помощи двойного интеграла, получим:

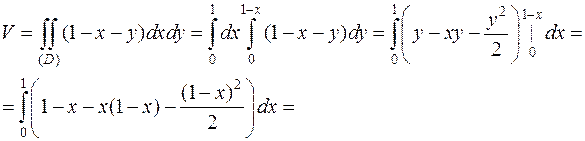
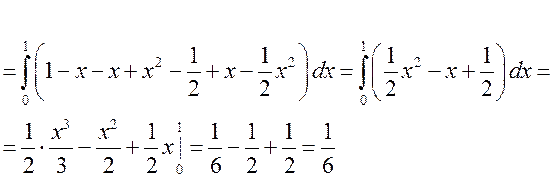
Итак, 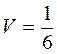(куб. ед.).

2.2. Вычисление площади кривой поверхности.

Пусть (σ) – участок поверхности 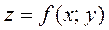, а область (D) – его проекция на координатную плоскость Oxy (рис. 11).

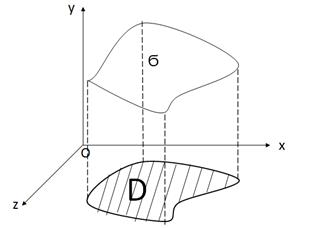
Рис. 11

Рис. 11

Тогда площадь участка поверхности (σ) вычисляют по формуле:

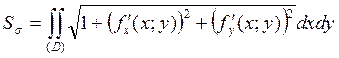
Пример

Вычислить площадь части параболоида вращения 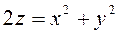, вырезанной цилиндром .

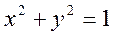Решение

Изобразим данную поверхность (рис. 12).

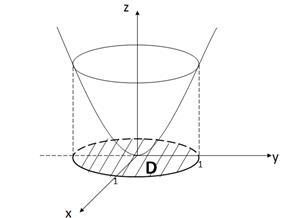
Рис. 12

Рис. 12

Проекцией этой поверхности на плоскость Oxy является область (D). Изобразим её в системе координат Oxy (рис. 13).

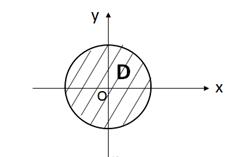Рис. 13

Из уравнения параболоида выделим z: 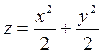. Значит, 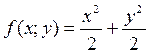. Найдём частные производные:

.

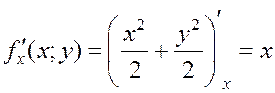
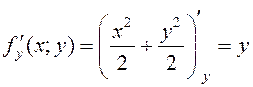Тогда

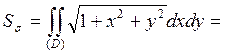
Для вычисления этого интеграла перейдём к полярным координатам: 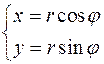, ,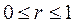