Принципы моделирования.

Рассмотрим основные принципы моделирования, в сжатой форме отражающие тот достаточно богатый опыт, который накоплен к настоящему времени в области разработки и использования математических моделей.

Принцип информационной достаточности. При полном отсутствии информации об исследуемой системе построение ее модели невозможно. При наличии полной информации о системе ее моделирование лишено смысла. Существует некоторый критический уровень априорных сведений о системе (уровень информационной достаточности), при достижении которого может быть построена ее адекватная модель.

Принцип осуществимости. Создаваемая модель должна обеспечивать достижение поставленной цели исследования с вероятностью, существенно отличающейся от нуля, и за конечное время. Обычно задают некоторое пороговое значение Р₀ вероятности достижения цели моделирования Р(t), а также приемлемую границу t₀ времени достижения этой цели. Модель считают осуществимой, если может быть выполнено условие Р(t₀) ≥ Р_0.

Принцип множественности. Данный принцип является ключевым. Речь идет о том, что создаваемая модель должна отражать в первую очередь те свойства реальной системы (или явления), которые влияют на выбранный показатель эффективности. Соответственно при использовании любой конкретной модели познаются лишь некоторые стороны реальности. Для более полного ее исследования необходим ряд моделей, позволяющих с разных сторон и с разной степенью детальности отражать рассматриваемый процесс.

Принцип агрегирования. В большинстве случаев сложную систему можно представить состоящей из агрегатов (подсистем), для адекватного математического описания которых оказываются пригодными некоторые стандартные математические схемы. Принцип агрегирования позволяет, кроме того, достаточно гибко перестраивать модель в зависимости от задач исследования.

Принцип параметризации. В ряде случаев моделируемая система имеет в своем составе некоторые относительно изолированные подсистемы, характеризующиеся определенным параметром, в том числе векторным. Такие подсистемы можно заменять в модели соответствующими числовыми величинами, а не описывать процесс их функционирования. При необходимости зависимость значений этих величин от ситуации может задаваться в виде таблицы, графика или аналитического выражения (формулы). Принцип параметризации позволяет сократить объем и продолжительность моделирования. Однако надо иметь в виду, что параметризация снижает адекватность модели.

7. Выбор различных видов моделей

Опр. Моделирование - это замещение исследуемого объекта (оригинала) его условным образом или другим объектом (моделью) и изучение свойств оригинала путем исследования свойств модели. Очевидно, что действительная польза от моделирования может быть получена только при соблюдении двух условий:

· модель обеспечивает корректное (или, как говорят, адекватное) отображение свойств оригинала, существенных с точки зрения исследуемой операции;

· модель позволяет устранить проблемы, присущие проведению измерений на реальных объектах.

В зависимости от способа реализации, все модели можно разделить на два больших класса: физические и математические.

Специальные виды моделей

• игровые – учитывающие действия противника

qмодели экономических ситуаций

qмодели военных действий

qспортивные игры

qтренинги персонала

• имитационные

• нельзя заранее вычислить или предсказать поведение системы;

• можно имитировать её реакцию на внешние воздействия;

• максимальный учет всех факторов;

Примеры:

qиспытания лекарств на мышах, обезьянах, …

qматематическое моделирование биологических систем

qмодели бизнеса и управления

qмодели процесса обучения

Модели по характеру связей

• детерминированные

связи между входными и выходными величинами жестко заданы

при одинаковых входных данных каждый раз получаются одинаковые результаты

Примеры

q движение тела, брошенного под углом к горизонту

q расчеты по известным формулам

q модель штатной работы механизма

• вероятностные (стохастические)

учитывают случайность событий в реальном мире

при одинаковых входных данных каждый раз получаются немного разные результаты

Примеры

q движение тела с учетом ветра

q броуновское движение частиц

q влияние волн на судно

q моделирование действий человека

Модели по фактору времени

• статические – описывают оригинал в заданный момент времени

qсилы, действующие на тело в состоянии покоя

qрезультаты осмотра врача

qфотография

• динамические

qмодель движения тела

qявления природы (молния, землетрясение, цунами)

8. Свойства нечетких множеств (которые позволяют применять их в задачах принятия решения)

Некоторые информационные системы имеют такие особенности, которые практически делают невозможным применение традиционных математических методов. Сложность процесса принятия решения, отсутствие математического аппарата приводят к тому, что при оценке и выборе альтернатив возможно использовать и обрабатывать качественную экспертную информацию. Перспективным направлением является лингвистический подход на базе теории нечетких множеств.Математическая статистика и теория вероятностей используют экспериментальные данные, обладающие строго определенной точностью и достоверностью. Теория нечетких множеств имеет дело с человеческими знаниями, которые принято называть экспертной информацией.

Основные понятия теории нечетких множеств.

Опр. Пусть Х ={ х } – универсальное множество, т.е. полное множество, охватывающее всю проблемную область. Нечеткое множество А есть набор пар 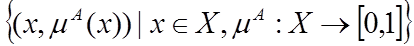, где 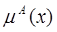– функция принадлежности которая является субъективной мерой соответствия элемента нечеткому множеству. Принимает значение от нуля (абсолютная непринадлежность) до единицы (абсолютная принадлежность) элемента х к А.

Если множество А определено на конечном универсальном множестве 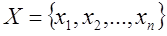, то его удобно обозначать 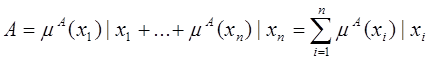где пара 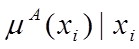– называется синглтоном.

Пример.

Пусть Х ={1, 2, ….10}. Тогда нечеткое множество «большие числа» может быть представлено как А =«большие числа»= 0.2|6+0.5|7+0.8|8+1|9+1|10. Это следует понимать: 9 и 10 с абсолютной уверенностью относятся к «большим числам», 8 есть большее со степенью 0.8 и т.д. 1, 2, …, 5 абсолютно не являются большими.

В случае непрерывного множества Х использую следующее обозначение нечеткого множества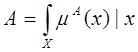

Операции над нечеткими множествами

1. Дополнением нечеткого множества А называют нечеткое множество 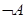, функция принадлежности которого равна .

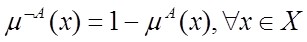2. Пересечением двух нечетких множеств A и 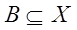называют нечеткое множество 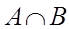, функция принадлежности которого равна 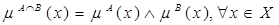, где – знак операции минимума.

3. Объединением двух нечетких множеств A и 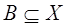называют нечеткое множество 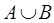, функция принадлежности которого равна 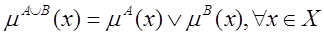, где – знак операции максимума.

9. Сравнение понятий планирование, прогнозирование, предсказание и предвидение

Планирование является информационным процессом. Особенность этого процесса – наличие временного сдвига информации выхода по отношению к информации входа. Входным является поток информации о прошлом (ретроспективная). Выходным является поток информации о будущем (перспективная).

Опр. Глубина ретроспекции – промежуток времени функционирования объекта в прошлом, по которому имеется необходимая и достаточная информация.

Опр. Глубина планирования – промежуток времени в будущем, на который разрабатывается план.

В зависимости от глубины планирования различают четыре этапа планирования:

1) оперативно-календарное (от 1 часа до 1 месяца);

2) текущее технико-экономическое (до 1 года);

3) перспективное и долгосрочное (до 15 лет);

4) прогнозирование

Первые три этапа составляют стадию разработки плана. С прогнозированием они имею общую сферу применения и одинаковый информационный поток. Принципиальное различие в том, что выходная информация в случае: план – директива; прогноз – ориентация.

Основные понятия теории прогнозирования Опр. Прогноз – это вероятностное суждение о состоянии объекта (процесса) в определенный момент времени в будущем или (и) альтернативных путях достижения цели.

Опр. Прогнозирование – это процесс формирования прогнозов развития объекта на основе анализа его развития.

Опр. Прогностика – наука, изучающая закономерности процесса прогнозирования.

Опр. Предсказание – достоверное, обоснованное на логической последовательности суждений о состоянии объекта в будущем.

Опр. Предвидение – опережающее отражение действительности, основанное на познании законов развития объекта. Следовательно, прогнозирование – «вероятно будет», предсказание - «будет», планирование – «должно быть».