
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Моделирование параллельных процессов.
|
|
Практически любая более или менее сложная система имеет в своем составе компоненты, работающие одновременно, или как принято говорить в технических науках, параллельно. Параллельно работающие подсистемы могут взаимодействовать самым различным образом, либо вообще работать независимо друг от друга. Способ взаимодействия подсистем определяет вид параллельных процессов, протекающих в системе. В свою очередь, вид моделируемых процессов влияет на выбор метода их имитации
Виды параллельных процессов.
Опр. Асинхронный параллельный процесс - это такой процесс, состояние которого не зависит от состояния другого параллельного процесса (ПП). Пример асинхронных ПП, протекающих в рамках одной системы, - подготовка и проведение рекламной кампании фирмой и работа сборочного конвейера. Или пример из области вычислительной техники - выполнение вычислений процессором и вывод информации на печать.
Опр. Синхронный ПП - это такой процесс, состояние которого зависит от состояния взаимодействующих с ним ПП. Пример синхронного ПП - работа торговой организации и доставка товара со склада (нет товара - нет торговли).
Один и тот же процесс может быть синхронным по отношению к одному из активных ПП и асинхронным по отношению к другому. Так, при работе вычислительной сети по технологии «клиент-сервер» каждый из узлов сети синхронизирует свою работу с работой сервера, но не зависит от работы других узлов.
Опр. Подчиненный ПП создается и управляется другим процессом (более высокого уровня). Весьма характерным примером таких процессов является ведение боевых действий подчиненными подразделениями.
Опр. Независимый ПП - процесс, который не является подчиненным ни для одного из процессов. Скажем, после запуска неуправляемой зенитной ракеты ее полет можно рассматривать как независимый процесс, одновременно с которым самолет ведет боевые действия другими средствами. Способ организации параллельных процессов в системе зависит сущности этой системы.
Остановимся несколько подробнее на особенностях реализации параллельных процессов в вычислительных системах (ВС). Это обусловлено следующей причиной. Разработка и использование любой ИМ предполагает ее программную реализацию и исследование с применением ВС. Поэтому для реализации моделей, имитирующих параллельные процессы, в некоторых случаях применимы механизмы, характерные для выполнения параллельных вычислений.
Языки реального времени (ЯРВ) - это языки, предназначенные для создания программного обеспечения, работающего в реальном масштабе времени, например для
разработки различных автоматизированных систем управления (предприятием, воздушным движением и т. д.).
17. Полно факторный эксперимент
Эксперимент на имитационной модели будем рассматривать состоящим из наблюдений, а каждое наблюдение – из прогонов модели.
Входные переменные х1, х2,..., хт называются факторами. Выходная переменная у называется наблюдаемой переменной (реакцией, откликом).
Факторное пространство - это множество факторов, значения которых исследователь может контролировать в ходе подготовки и проведения модельного эксперимента.
Каждый фактор имеет уровни. Уровни - это значения, которые устанавливаются для каждого фактора при определении условий прогона модели в наблюдении.
Эксперимент, в котором реализуются все возможные сочетания уровней факторов, называется полным факторным экспериментом (ПФЭ).
Эксперимент, в котором реализуются все возможные сочетания уровней факторов называется полным факторным экспериментом (ПФЭ).
Общее число различных комбинаций уровней в ПФЭ для k факторов можно вычислить так:
N = l1× l2× l3× …× lk×
Здесь li - число уровней i-го фактора.
Если число уровней для всех факторов одинаково, то N=Lk (L - число уровней). Недостаток ПФЭ - большие временные затраты на подготовку и проведение. Например, если в модели отражены 3 фактора, влияющие на значение выбранного показателя эффективности, каждый из которых имеет 4 возможных уровней (значения), то план проведения ПФЭ будет включать 64 эксперимента (N=43). Если при этом каждый из них длится хотя бы одну минуту (с учетом времени на изменение значений факторов), то на однократную реализацию ПФЭ потребуется более часа.
Поэтому использование ПФЭ целесообразно только в том случае, если в ходе имитационного эксперимента исследуется взаимное влияние всех факторов, фигурирующих в модели.Если такие взаимодействия считают отсутствующими или их эффектом пренебрегают, проводя частичный факторный эксперимент (ЧФЭ).Пусть в эксперименте используется первичный фактор А и два вторичных фактора – В и С, число уровней факторов l равно 4. Соответствующий план можно представить в виде квадратной матрицы размером l× l (4× 4) относительно уровней фактора А. При этом матрица строится таким образом, чтобы в каждой строке и в каждом столбце данный уровень фактора А встречался только один раз:
| Значение фактора В | Значение фактора С | |||
| С1 | С2 | С3 | С4 | |
| В1 | А1 | А2 | А3 | А4 |
| В2 | А2 | А3 | А4 | А1 |
| В3 | А3 | А4 | А1 | А2 |
| В4 | А4 | А1 | А2 | А3 |
В результате имеем план, требующий 4× 4=16 прогонов, в отличие от ПФЭ, для которого нужно 43=б4 прогона.
18. Методы понижения дисперсии
Основной недостаток методов планирования, основанных на использования простой случайной выборки, - медленная сходимость выборочных средних к истинным средним с ростом объема выборки NT (пропорционально значению квадратного корня из NT). Это приводит к необходимости использования методов уменьшения ошибок, не требующих увеличения NT. Такие методы называются методами понижения дисперсии и делятся на три группы:
· активные (предусматривают формирование выборки специальным образом);
· пассивные (применяются после того, как выборка уже сформирована);
· косвенные (в которых для получения оценок наблюдаемой переменной и используются значения некоторых вспомогательных величин).
На практике снижения влияния переходного периода обычно добиваются одним из
следующих способов:
· методом повторения;
· методом подинтервалов;
· методом цикла.
Метод повторений. При использовании этого метода каждое наблюдение получается при помощи отдельного прогона модели, причем все прогоны начинаются при одних и тех же начальных условиях, но используются различные последовательности случайных чисел.
Преимуществом метода является статистическая независимость получаемых наблюдений. Недостаток состоит в том, что наблюдения могут оказаться сильно смещенными под влиянием начальных условий.
Метод подинтервалов. Данный метод основан на разбиении каждого прогона модели на равные промежутки времени. Начало каждого интервала совпадает с началом очередного этапа наблюдений.
Достоинство метода состоит в том, что влияние переходных условий со временем уменьшается, и наблюдения точнее отражают поведение системы в стационарном режиме. Недостаток - значения наблюдаемых переменных, полученные в начале очередного интервала, зависят от конечных условий предыдущего интервала (то есть между интервалами существует автокорреляция).
Метод циклов. При использовании метода циклов влияние автокорреляции уменьшается за счет выбора интервалов таким образом, чтобы в их начальных точках условия были одинаковыми.
Метод стратифицированной выборка. Данный метод относится к группе пассивных
методов понижения дисперсии. Пассивные методы влияют на подготовку и проведение эксперимента, но реализуются на этапе обработки и анализа результатов моделирования.
Косвенные методы понижения дисперсии основаны на том, что зачастую некоторые из выходных характеристик модели получить (вычислить) легче, чем другие. Их использование предполагает не только весьма глубокое знание сущности процесса, протекающих в системе, но и наличие формального описания взаимной зависимости параметров модели.
19. Спектор Фурье и Вейвлет анализ
В основе любого из множества разработанных для этой цели методов лежит вычисление некоторого количества коэффициентов ряда Фурье периодической функции 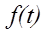 :
:
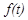 ~
~ 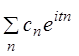 (1)
(1)
Эта функция получается из исходного сигнала путем сглаживания, усреднения по определенным образом выбираемым сегментам, и тому подобными операциями. Характер изменения коэффициентов позволяет получить ценную информацию о свойствах сигнала – например, выявить скрытые периоды. Для вычисления коэффициентов существует быстрый алгоритм, требующий ~ 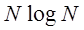 операций, где N – длина сигнала. Важнейшим свойством коэффициентов Фурье является то, что каждый из них отражает поведение
операций, где N – длина сигнала. Важнейшим свойством коэффициентов Фурье является то, что каждый из них отражает поведение 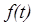 в целом. Спектр Фурье наглядно демонстрирует лишь глобальные свойства сигналов, но из него трудно извлечь информацию о локальных особенностях – резких скачках, узких пиках, и т.п.
в целом. Спектр Фурье наглядно демонстрирует лишь глобальные свойства сигналов, но из него трудно извлечь информацию о локальных особенностях – резких скачках, узких пиках, и т.п.
Причина этого в строении базисных функций 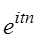 . Каждая из них «размазана» по всему интервалу изменения функции, поэтому коэффициенты, имеющие вид
. Каждая из них «размазана» по всему интервалу изменения функции, поэтому коэффициенты, имеющие вид
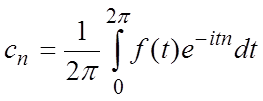 (2)
(2)
зависят от значений функции на всем интервале.
Вейвлет-анализ – это исследование сигнала 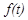 при помощи вычисления величин, аналогичных (2), но с другими «пробными функциями». Сигнал
при помощи вычисления величин, аналогичных (2), но с другими «пробными функциями». Сигнал 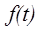 интерпретируется, как функция из
интерпретируется, как функция из 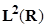 , а вместо гармоник
, а вместо гармоник 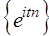 используется система функций
используется система функций 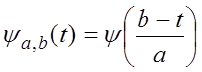 , занумерованных не целыми числами, а двумя непрерывными параметрами. Эта система получается из фиксированной функции
, занумерованных не целыми числами, а двумя непрерывными параметрами. Эта система получается из фиксированной функции 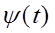 всевозможными сдвигами и растяжениями. Функция
всевозможными сдвигами и растяжениями. Функция 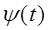 называется вейвлетом (по-английски – wavelet; в русской математической литературе используется также термин всплеск), если:
называется вейвлетом (по-английски – wavelet; в русской математической литературе используется также термин всплеск), если:
A. 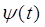 непрерывна;
непрерывна;
B. 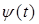 интегрируема на всей прямой;
интегрируема на всей прямой;
C. 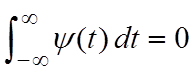
Вейвлет-преобразованием 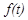 называется функция двух переменных
называется функция двух переменных
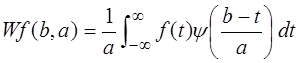 (3)
(3)
Итак, в отличие от преобразования Фурье, вейвлет-преобразование определено неоднозначно: каждому вейвлету соответствует свое преобразование. Условие С означает, что Фурье-образ 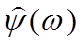 вейвлета обращается в 0 при
вейвлета обращается в 0 при 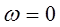 ; это нужно для того, чтобы в Фурье-области вейвлет был локализован вокруг некоторой ненулевой частоты
; это нужно для того, чтобы в Фурье-области вейвлет был локализован вокруг некоторой ненулевой частоты 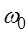 .
.
20. Дискретное время
Время
Ньютоновская модель времени родилась при формулировании законов классической механики. В представлении Ньютона время является самостоятельной сущностью реального мира, что позволяет говорить о его математических моделях. Ньютон различал:
· физическое (астрономическое) время: «… относительное, кажущееся или обыденное время есть или точная, или изменчивая, постигаемая чувствами, внешняя, совершаемая при посредстве какого-либо движения, мера продолжительности, употребляемая в обыденной жизни вместо истинного математического времени, как то час, день, месяц, год»;
· абсолютное (математическое) время: «Абсолютное, истинное математическое время само по себе и по своей сущности, без всякого отношения к чему-либо внешнему, протекает равномерно и иначе называется длительностью».
В абсолютном непрерывном времени не возникает проблем с синхронизацией параллельно протекающих процессов. При рассмотрении многих реальных физических процессов часто отказываются от свойства непрерывности времени и вводят дискретное время. Под дискретным временем понимают любую упорядоченную, неограниченно возрастающую последовательность вещественных или рациональных чисел, {t0, t1, …, tk, … },
а чаще всего множество целых чисел.
Аналогично тому, как непрерывное время является независимой переменой в дифференциальных уравнениях, дискретное время играет роль независимой переменной в разностных уравнениях.
Дискретное время естественным образом появляется там, где наблюдается деление поведения на «быстрые» (дискретные или мгновенные действия) и «медленные» (непрерывные или длительные) действия.
При использовании дискретного времени проблема синхронизации становится более сложной. Предположим что две последовательности с несовпадающими отсчетами являются «часами» двух независимых систем. Тогда если мы хотим рассматривать одновременно работу двух систем, придется вводить новые единые часы. Этого можно достигнуть, например, доопределяя значения переменных на несовпадающих временных точках.
Рассмотрим пример. Пусть два любителя обмениваться сообщениями с помощью «азбуки Морзе» могут выходить в эфир только в определенные моменты времени, а в каждый такт либо посылать сигналы, либо получать их. Если они не договорятся о синхронизации часов, услышать друг друга им вряд ли удастся. Если они синхронизируют часы, но выберут несоизмеримые такты - результат будет тем же. Если они синхронизируют часы и выберут соизмеримые, но не совпадающие такты - часть сообщений пропадет. Для правильной работы нужно синхронизировать часы, выбрать равные такты и поочередно на одном такте принимать чужие сигналы, а на следующем - отвечать на них. Но проще всего запоминать полученные сигналы (фиксировать их значения между тактами), и тогда проблема синхронизации исчезнет.
21. Свойства устойчивости и чувствительности модели