Порядок выполнения работы. Приборы и принадлежности

Приборы и принадлежности

Маятник Максвелла с жестким закреплением диска на оси вращения с известной массой, съемные кольца с известной массой, линейка, секундомер.

Краткая теория

В работе изучается общее движение твердого тела. Любое сложное движение можно представить как сумму простых, при этом скорость общего движения определяется суммой скоростей простых движений.

В случае общего движения твердого тела оно может быть разделено на поступательное и вращательное. В то же время общее движение твердого тела можно рассматривать как вращательное движение относительно мгновенной оси (прямой, проходящей через точку твердого тела, которая в данный момент оказывается неподвижной). Мгновенная ось с течением времени непрерывно перемещается как в теле, так и в пространстве. Такое описание общего движения обосновывается теоремой Эйлера.

Рассмотрим оба случая на примере движения цилиндра по наклонной плоскости (рис. 1).

Если цилиндр радиусом r скатывается без скольжения, то составляющая силы тяжести вызывает два движения: ускоренное перемещение цилиндра вдоль плоскости как прямолинейное движение и ускоренное вращательное движение цилиндра относительно своей оси.

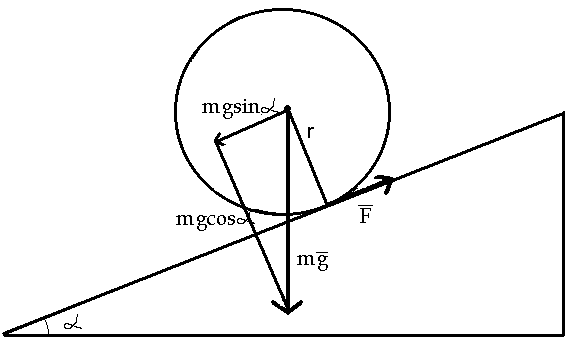
Рис. 1

Второй механизм описания предлагает рассматривать движение цилиндра как ускоренное вращение вокруг мгновенной оси, которая в данный момент проходит через точку А, так как она неподвижна (цилиндр скатывается без скольжения). В следующий момент времени точка касания сместится в другое место пространства.

Рассчитываем ускорение поступательного движения свободно скатывающегося цилиндра, используя закон вращательного движения

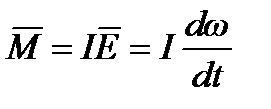(1)

где M = [rF] – момент силы F, r – плечо силы; I – момент инерции тела относительно выбранной оси; e - угловое ускорение; w – угловая скорость.

Закон вращательного движения имеет форму написания в точности такую же, как и второй закон Ньютона для поступательного движения

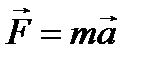. (2)

Можно сказать, что изменяя F на M, m на I и а на e мы перешли из поступательного движения к вращательному. Такой подход полезен тем, что опыт решения задач на поступательное движение формально полностью реализуется при анализе вращательного движения. В соответствии с рис. 1 момент силы будет

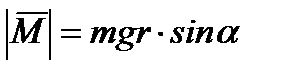, (3)

подставим (3) в (1) и получим

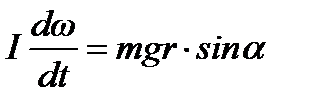. (4)

Обозначим через u линейную скорость точки О относительно мгновенной оси А

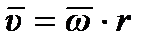, (5)

дифференцируя по t, получим

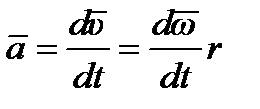, (6)

выражая из формулы (4) значение dw/dt и подставляя в (6) получим

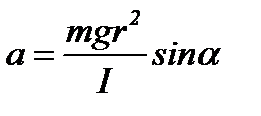. (7)

Это соотношение хорошо используется в связи двух видов движения. Видно, что чем больше будет момент инерции, тем меньше будет ускорение поступательного движения скатывания при прочих неизменных условиях. Осуществить такой случай можно с помощью диска Максвелла, который представляет собой диск, посаженный на цилиндрическую ось, закрепленную на бифилярном подвесе. Такое движение полностью адекватно рассмотренному скатыванию по наклонной плоскости под углом a = 90 ^о. При таком движении изменяется только момент инерции диска I_o= (m_o R²)/2, а остальные параметры формулы (7) остаются постоянными.

Используя маятник Максвелла, можно экспериментально изучать законы общего движения твердого тела.

Конструкция установки " Маятник Максвелла"

Общий вид маятника Максвелла показан на рис. 2.

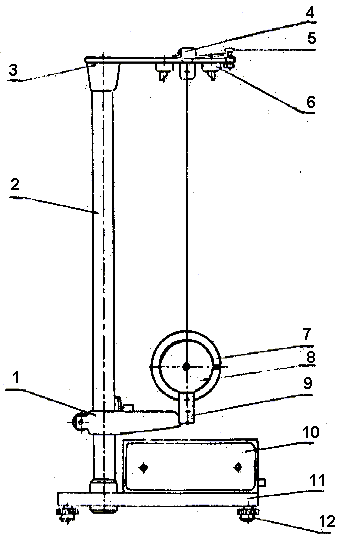
Рис. 2

Основание (11) оснащено регулируемыми ножками (12), которые позволяют произвести горизонтирование прибора.

В основании закреплена колонка (2), к которой прикреплен неподвижный верхний кронштейн (3) и подвижный нижний кронштейн (1), электронный секундомер (11). На верхнем кронштейне находится электромагнит (6), фотоэлектрический датчик (4) и вороток (5) для закрепления и регулирования длины бифилярной подвески маятника.

Нижний кронштейн вместе с прикрепленным к нему фотоэлектрическим датчиком (9) можно перемещать вдоль колонки и фиксировать в произвольно выбранном положении. Диск Максвелла (8), закрепленный бифулярным подвесом, позволяет менять его момент инерции при помощи сменных колец (7).

Диск с наложенным кольцом удерживается в верхнем положении электромагнитом. Длина маятника определяется по миллиметровой шкале на колонке прибора (от нижней кромки кольца (7) в верхнем положении диска Максвелла, до нижней кромки кольца в нижнем положении диска). С целью облегчения этого измерения нижний кронштейн оснащен указателем.

Для подготовки прибора к работе необходимо:

- проверить заземление прибора;

- проверить вертикальность прибора;

- включить сетевой шнур в питающую сеть;

- нажать клавишу " сеть", проверяя, произошло ли высвечивание цифровыми индикаторами нулей и засветились ли лампочки фотоэлектрических датчиков.

Прибор готов к работе непосредственно после подключения к питающей цепи.

Порядок выполнения работы

Задание 1.1. Определение момента инерции диска Максвелла