Імовірнісний метод

Метрологічне забезпечення обумовлює форми представлення результатів вимірів. Найбільш поширеною формою представлення точності виміру є інтервал із нижньої D₁ і верхньої D₂ межами, у якому з заданою довірчою ймовірністю. Р знаходиться сумарна похибка виміру D. Результати виміру Х:

X, D; D₁ ...D₂; Р.

Наприклад: 10 В, D; -0, 5... +0, 5 В; Р = 0, 99.

Імовірнісній метод базується на визначенні зазначених величин при багатократних вимірах. Обробку результатів спостережень проводять в наступній послідовності: вилучення з отриманого ряду спостережень промахів; визначення основних числових характеристик виправленого ряду спостережень; перевірку гіпотези про нормальний закон розподілу; ймовірністну оцінку похибки вимірів.

Промахи - значення вимірюваної величини, що значно відрізняються від всіх інших значень ряду, - є слідством несправності засобу виміру, помилкового зчитування показань, їхнього запису та ін. Промахи просто вилучаються зі значень ряду.

Систематичною похибкою називають складову похибки вимірів, що при повторенні рівноточних вимірів розміру з незмінним розміром залишається постійною або закономірно змінюється

У більшості випадків випадкові похибки підпорядковуються нормальному закону розподілу. Нормальний закон розподілу задається цілком

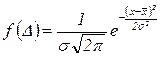, (1.1)

де f( D ) - щільність розподілу ймовірностей;

D - випадкова похибка;

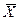- математичне очікування /середнє значення/ вимірюваної величини;

s - середньоквадратичне відхилення випадкової похибки відїї математичного очікування.

Для більш достовірної оцінки випадкової похибки при малому числі n вимірів ряду при нормальному законі розподілу вводять коефіцієнт Стьюдента t(n).

Для знаходження t(n) необхідно знати число вимірів n і довірчу ймовірність Р( D ). Довірча ймовірність - це ймовірність того, що випадкова похибка D не виходить за деякі межі [D₁, D₂]. Інтервал між цими межами називається довірчим інтервалом. У практиці вимірювань користуються інтервалом [+3s, -Зs]. Довірча можливість при нормальному законі розподілу визначається в такий спосіб:

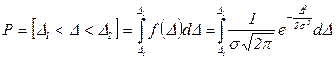, (1.2)

при ;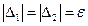

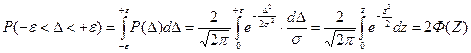, (1.3)

де , ;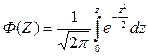

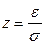Ф(z) - функція Лапласа /інтеграл ймовірностей/, значення якої табульовані.

Похибці 3s відповідає довірча імовірність Р(D)= 0, 9973.

Межа довірчого інтервалу похибки з урахуванням коефіцієнта Стьюдента оцінюється при

D₁=D₂=e; 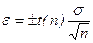; (1.4)

а результат вимірювань може бути записаний

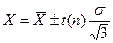, (1.5)

Для імовірнісної оцінки результатів прямих вимірювань можна рекомендувати таку послідовність:

1. Визначення всіх n значень ряду вимірювань Х₁, Х₂, X3, …, Хn.

2. Обчислення середнього значення .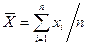

3. Визначення випадкових відхилень r₁, r₂, r₃, …, r_n, де 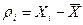(з урахуваннямзнака) (1.6).

4. Розрахунок середньоквадратичного відхилення

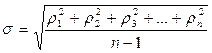. (1.7)

5. Визначення довірчої ймовірності Р(D) = 2Ф(Z), де Ф(Z) - інтеграл ймовірностей, визначається з урахуванням меж довірчого інтервалу.

6. Знаходження коефіцієнта Стьюдента t(n) по відомим n і Р(D).

7. Розрахунок граничного значення випадкової похибки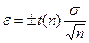

8. Запис отриманого результату вимірювань 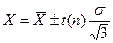.