Усеченное нормальное распределение

Плотность усеченного нормального распределения имеет следую­щий вид:

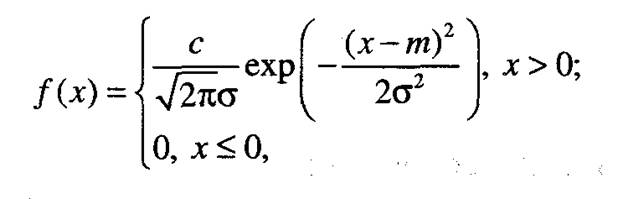
здесь 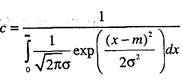- нормировочная константа.

Функция распределения равна

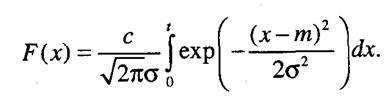
Будем обозначать 9, - математическое ожидание, 9₂ - среднее квадратическое отклонение. Рассмотрим последовательно вычисление оценок параметров для различных схем наблюдений.

1. Функция правдоподобия для полных наработок имеет вид

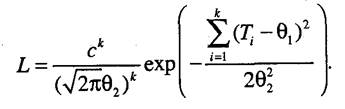
Соответствующая логарифмическая функция правдоподобия

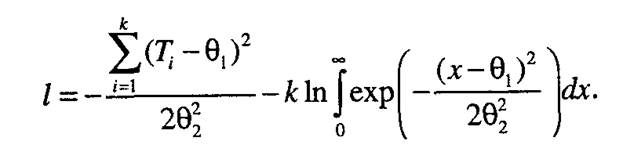
Обозначим: 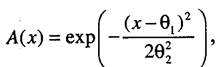тогда

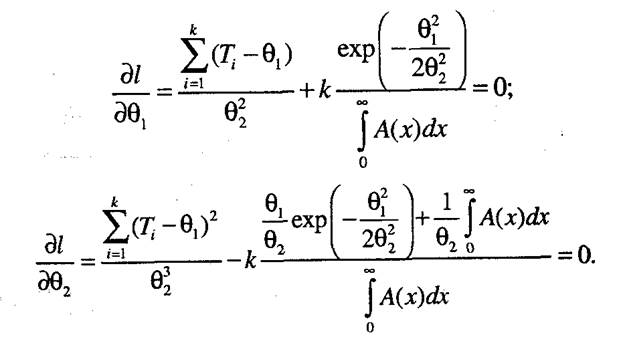
Решая данную систему уравнений, получаем оценки параметров усе­ченного нормального закона распределения для случая полных нарабо­ток.

2. Для выборок, содержащих полные и цензурированные справа на­работки, функцию правдоподобия можно записать

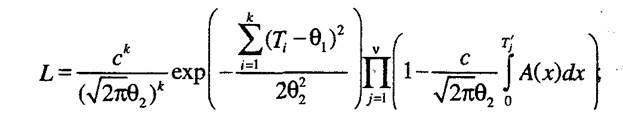
логарифмическая функция правдоподобия равна

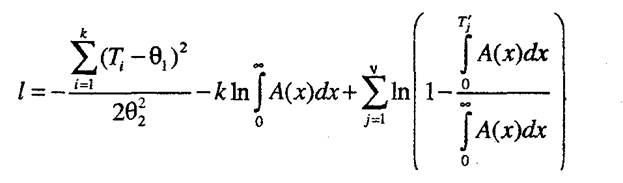
И, наконец, производные по параметрам определим следующим обра­зом:

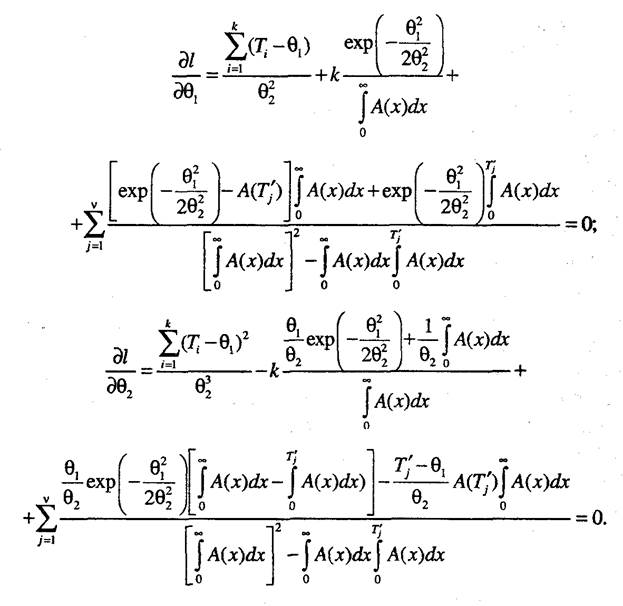
3. Для выборок, содержащих полные и цензурированные слева на­работки, функция правдоподобия записывается

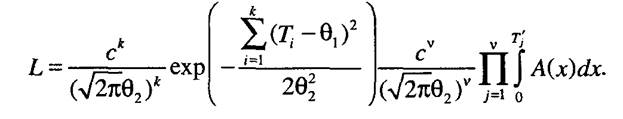
Далеевычисляем логарифмическую функцию

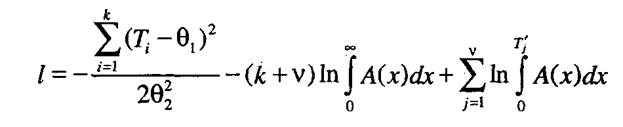
и производные для вычисления оценок параметров

4. Для группированных данных итоговые оценки получаются таким образом.

Функция правдоподобия имеет вид

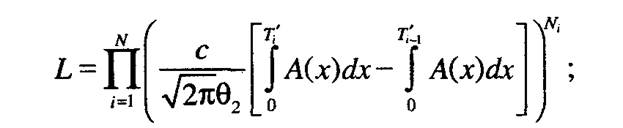
логарифмическая функция правдоподобия:

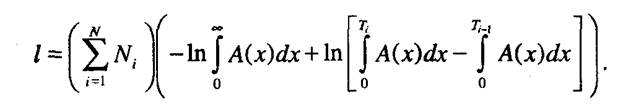
Производные по параметрам равны

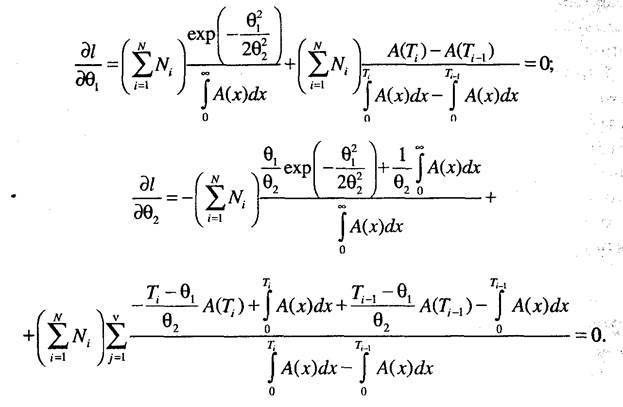
Как видно из приведенных выражений, для определения парамет­ров усеченного нормального закона распределения необходимо решать систему уравнений численными методами.