
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Объёмный расход газа на входе одноступенчатого
|
|
КОМПРЕССОРА
Так же, как объёмную подачу объёмного насоса, значение 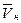 для поршневого компрессора можно определить по секундному (или минутному) рабочему объёму, описываемому поршнями первой ступени в единицу времени:
для поршневого компрессора можно определить по секундному (или минутному) рабочему объёму, описываемому поршнями первой ступени в единицу времени:
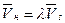 , (15.1)
, (15.1)
К о э ф ф и ц и е н т о б ъ ё м н о г о р а с х о д а г а з а н а в х о д е λ отражает влияние нескольких факторов. Из рис. 15.2 видно, что газ поступает в рабочую камеру не только из всасывающей линии, но также перетекает из областей высокого давления через неплотности клапанов и поршня, вследствие чего масса газа  , отбираемого из всасывающей линии, меньше массы газа, поступившей в цилиндр к концу хода всасывания (точка a на индикаторной диаграмме, рис. 15.1, a). Соответствующие массовые расходы связаны равенством
, отбираемого из всасывающей линии, меньше массы газа, поступившей в цилиндр к концу хода всасывания (точка a на индикаторной диаграмме, рис. 15.1, a). Соответствующие массовые расходы связаны равенством
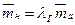 , (15.2)
, (15.2)
где λ Г - коэффициент герметичности.
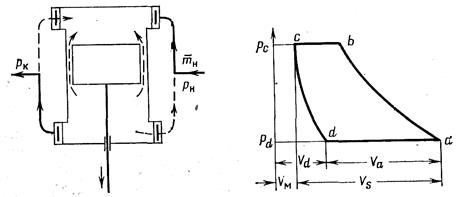
Рис. 15.2. Схема перетечек газа Рис. 15.3. К определению объёмного
в компрессоре коэффициента
Согласно уравнению Клапейрона для идеального газа:
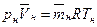 ;
; 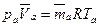 . (15.3)
. (15.3)
Подставим (15.3) в (15.2) и разделим обе части равенства на 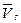
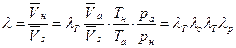 , (15.4)
, (15.4)
где λ о– объёмный коэффициент; λ T– коэффициент подогрева; λ p – коэффициент давления.
Из схематизированной индикаторной диаграммы на рис. 15.3 видим, что объём газа, поступившего в цилиндр, меньше объёма цилиндра на объём расширившегося «мёртвого» остатка1:
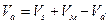 . (15.5)
. (15.5)
Объём V d определим из уравнения политропы расширения с показателем n р (газ идеальный):
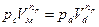 . (15.6)
. (15.6)
Подставив значение V d в выражение (15.5) и обозначив относительный объём «мёртвого» пространства 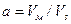 , получим формулу
, получим формулу
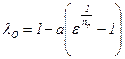 , (15.7)
, (15.7)
поскольку 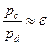 . Для краткости относительный объём a будем называть клиренсом.
. Для краткости относительный объём a будем называть клиренсом.
Показатель политропы при расширении ниже, чем при сжатии. Ориентировочные его значения при ε = 3 – 4 приведены в табл. 15.1.
Таблица 15.1
| p н, МПа | n p | p н, МПа | n p |
| До 0, 15 | 1 + 0, 50 (k – 1) | От 1, 0 до 3, 0 | 1 + 0, 88 (k – 1) |
| От 0, 15 до 0, 40 | 1 + 0, 62 (k – 1) | Свыше 3, 0 | k |
| От 0, 40 до 1, 0 | 1 + 0, 75 (k – 1) |
Определить коэффициент λ по формуле (15.4) затруднительно, так как кроме λ Онеобходимо иметь значения трёх коэффициентов λ Г, λ T, λ p. Их можно объединить в общий коэффициент эффективности всасывания, определяемый по эмпирической формуле В. Е. Лисичкина и А. М. Горшкова:
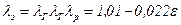 . (15.8)
. (15.8)
Более простой путь – использование опытных формул для определения непосредственно коэффициента λ, одна из которых имеет следующий вид:
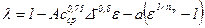 . (15.9)
. (15.9)
Здесь A – коэффициент, равный 0, 007 для крупных компрессоров и 0, 008 для малых компрессоров; 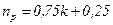 для c ср = 3 м / с;
для c ср = 3 м / с; 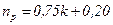 для c ср = 1, 5 м / с;
для c ср = 1, 5 м / с;
c ср – средняя скорость поршня (c ср = 2 Sn); ∆ - относительная плотность газа по воздуху; остальные обозначения прежние.
Иногда используются опытные формулы следующего вида:
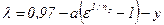 , (15.10)
, (15.10)
где поправка 0, 97 введена для учёта подогрева газа, а коэффициентом y = 0, 02 – 0, 05 учитываются объёмы газа, перетекающего через неплотности рабочих камер.
Наряду с приведенными формулами, объёмный расход газа на входе в компрессор можно определить по опытным графикам, полученным при испытании компрессора (рис. 15.4).
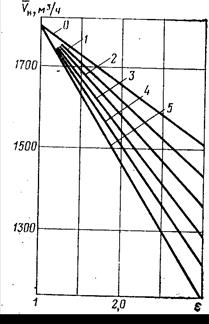
15.4. График объёмного расхода на входе в компрессор
при включении дополнительных «мёртвых» пространств (карманов)
0 – все карманы закрыты; 1 – 5 – открыты карманы: один, два и т. д.
Каждая линия графика зависимости ε - 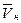 относится к определённому объёму «мёртвого» пространства, который регулируется.
относится к определённому объёму «мёртвого» пространства, который регулируется.
Выражение (15.7) уточним для реального газа с учётом того, что для начала и конца расширения остатка газа
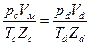 .
.
Следовательно, для вычисления объёмного коэффициента необходимо знать температуру остатка газа в начале расширения T c. Обычно её принимают равной конечной температуре газа T к, которую при высоких давлениях без особой ошибки можно определять по формуле адиабатического сжатия идеального газа
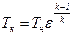 , (15.11)
, (15.11)
причём 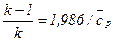 , где
, где 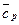 - молярная теплоёмкость газа, которую рекомендуется брать для стандартных условий, чтобы тем самым компенсировать погрешность в результатах при использовании формулы (15.11) для реального газа.
- молярная теплоёмкость газа, которую рекомендуется брать для стандартных условий, чтобы тем самым компенсировать погрешность в результатах при использовании формулы (15.11) для реального газа.
Приняв приближённо: Z d ≈ Z н; Z c ≈ Z к; T d ≈ T н; p c / p d ≈ ε, получим объём расширившегося «мёртвого» остатка:
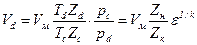 ,
,
а затем
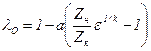 . (15.12)
. (15.12)