
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
г.Обнинск, 2014 г.
|
|
Лабораторная работа №3
Частотный анализ типовых звеньев
Вариант 6
Выполнил
Студент 4 курса Зарапин Г. О.
группы ЭиА-С11
Проверил: Мурачев Е.Г.
г.Обнинск, 2014 г.
Цели работы: освоение методов анализа линейных систем с помощью программы Vissim; изучение частотных характеристик типовых линейных звеньев.
Задание к работе: 1. Записать выражения для W(jw), 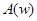 ,
, 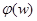 ,
, 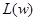 , с учетом коэффициентов вашего варианта для каждого из трех типовых динамических звеньев.
, с учетом коэффициентов вашего варианта для каждого из трех типовых динамических звеньев.
2. Построить графики АЧХ, ЛАЧХ, ФЧХ, ЛФЧХ и АФЧХ(годограф Найквиста) для каждого их трех типовых динамических звеньев. Изучить влияние параметров звена на общий вид графиков. Указать на графиках и записать координаты точек сопряжения и среза. На графике АФЧХ указать направление обхода.
3. Записать передаточную функцию для заданного дифференциального уравнения. Построить для нее ЛАЧХ, ЛФЧХ и АФЧХ.
4. Сделать вывод о проделанной работе.
Ход работы:
1) Диссипативное колебательное звено:
- cтатическая характеристика - X = K× U;
- уравнение движения - T2× [d 2 X(t)/dt2] + 2× x× T× [dX(t)/dt] + X(t) = K× U(t);
- передаточная функция - W(s) = K/(T2s2 + 2× x× Ts + 1);
- переходная функция - H(t) = K× [1-exp(-tx/T)× cos(A× 2× p× t)-B× sin(A× 2× p× t)],
где A = [(1- x2)1/2]/T, B = x/[(1- x2)1/2];
- весовая функция - W(t) = K× B× exp(-tx/T)× sin(A2pt)/T;
- амплитудно-частотная характеристика –
- А(w) = K/{[(1-T2× w2)2 + 4× x2× T2× w2 ]1/2};
- фазо-частотная характеристика - F(w) = - arctg[2× x× T× w/(1 - T2× w2)],
при 1-T2× w2 = 0: F(w) = - p/2,
при 1-T2× w2 < 0: F(w) = F(w) - p;
- aмплитудно-фазо-частотная характеристика –
W(jw) = (1 - T2× w2)/[(1 - T2× w2)2 + 4× x2× T2× w2] -
- j 2× K× x× T× w/[(1 - T2× w2)2 + 4× x2× T2× w2];
- логарифмическая амплитудно-частотная характеристика -
- L(w) = 20× lg(K) - 20× lg{[(1 - T2× w2)2 + 4× x2× T2× w2]1/2}.
K = 7; T = 0.2; x = 0.5
передаточная функция - W(s) = 7/(0.04s2 + 0.2s + 1)
1.1. Комплексный коэффициент передачи (ККП) диссипативного колебательного звена
W(j w ) = (1 - T2 × w 2)/[(1 - T2 × w 2)2 + 4 × x 2 × T2 × w 2] -- j 2 × K × x× T × w /[(1 - T2 × w 2)2 + 4 × x 2 × T2 × w 2];
W(j w ) = (1 – 0.042 × w 2)/[(1 – 0.042 × w 2)2 + 0.04 × w 2] -- j 1.4 × w /[(1 – 0.042 × w 2)2 + 0.04 × w 2];
1.2. Выражения для АЧХ, ФЧХ, ЛАЧХ
АЧХ: А(w) = K/{[(1-T2× w2)2 + 4× x2× T2× w2 ]1/2} = 7/{[(1-0.042× w2)2 + 0.04× w2 ]1/2};
ФЧХ: F(w) = - arctg[2× x× T× w/(1 - T2× w2)] =- arctg[0.2× w/(1 – 0.04× w2)]
при 1-T2× w2 = 0: F(w) = - p/2,
при 1-T2× w2 < 0: F(w) = F(w) - p;
ЛАЧХ: L(w) = 20× lg(K) - 20× lg{[(1 - T2× w2)2 + 4× x2× T2× w2]1/2}= 20× lg(7) - 20× lg{[(1 – 0.04× w2)2 + 0.04× w2]1/2}.
1.3. На рабочем поле собрал схему, состоящую из генератора ступенчатого сигнала, диссипативного колебательного звена и осциллографа, получил график переходного процесса.
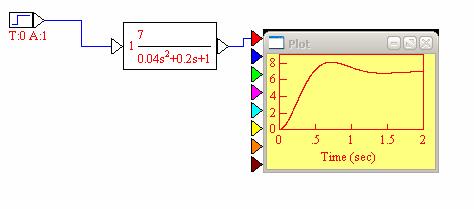
Рис. 1. Переходной процесс диссипативного колебательного звена
1.4. Построил ЛАЧХ и ЛФЧХ диссипативного колебательного звена.
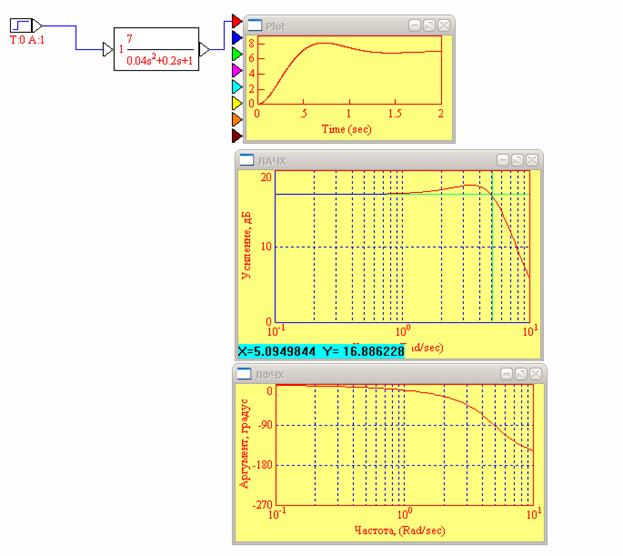
Рис. 2. ЛАЧХ и ЛФЧХ диссипативного колебательного звена при T=0.2; K=7
20lgK=20lg7=16.9
ω ср=8 рад/с
ω с=5, 09 рад/с (ω c=1/T=1/0.2=5)
k=1016.9/20=6.998≈ 7
Изменил сначала значение коэффициента усиления (K=5)
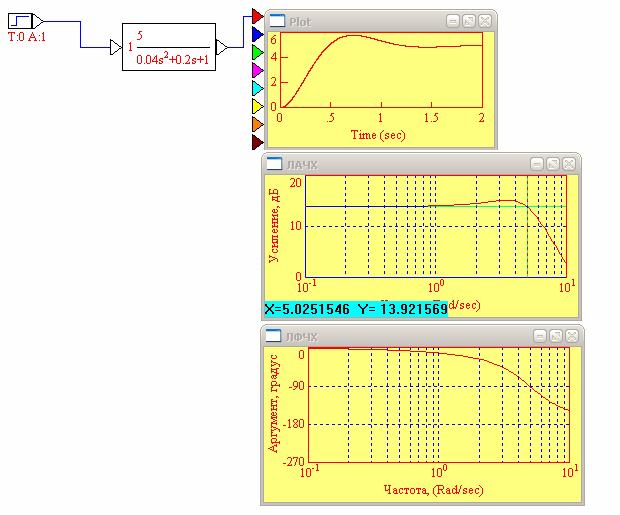
Рис. 3. ЛАЧХ и ЛФЧХ диссипативного колебательного звена при T=0.2; K=5
20lgK=20lg5=13.98
ω ср=7 рад/с
ω с=5, 02рад/с (ω c=1/T=1/0.2=5)
k=1013.98/20=5
Изменил значение постоянной времени (T=0.5)
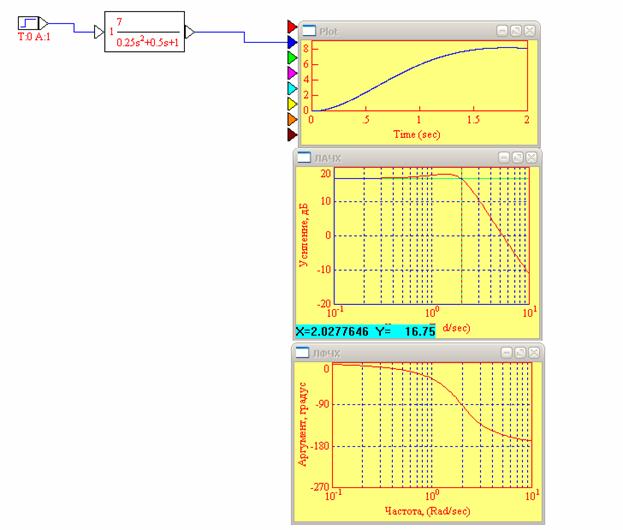
Рис. 4. ЛАЧХ и ЛФЧХ диссипативного колебательного звена при T=0.5; K=7
20lgK=20lg7=16.9
ω ср=5.4 рад/с
ω с=2, 03 рад/с (ω c=1/T=1/0.5=2)
k=1016.9/20=6.998≈ 7
1.4. Построил амплитудно-фазовую частотную характеристику АФЧХ (или годограф Найквиста) для диссипативного колебательного звена.
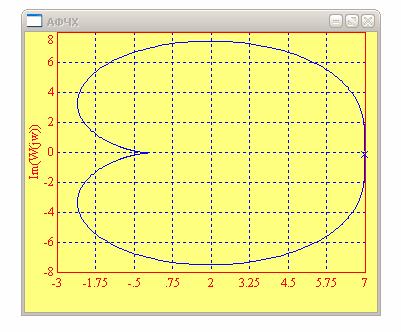
Рис. 5. АФЧХ диссипативного колебательного звена
Вывод:
В ходе исследования диссипативного колебательного звена я получил: комплексный коэффициент передачи (ККП), выражения для АЧХ, ФЧХ, ЛАЧХ, график переходного процесса(рис.1). Построил ЛАЧХ и ЛФЧХ диссипативного колебательного звена при разных вариациях коэффициента усиления и постоянной времени. При каждой вариации по графикам определял частоту среза, частоту сопряжения и коэффициент усиления (рис. 2 – рис. 4). При изменении коэффициента усиления частота среза менялась, а частота сопряжения оставалась неизменной. При изменении постоянной времени менялась частота сопряжения и частота среза. Коэффициент усиления оставался неизменным. При всех вариациях заметней всего менялась ЛФЧХ. При всех вариациях практическая частота сопряжения была близка к теоретическим значениям. Построил амплитудно-фазовую частотную характеристику АФЧХ (или годограф Найквиста) для диссипативного колебательного звена. Указал направление обхода контура (рис. 5). Определил асимптотическую ЛАЧХ колебательного звена
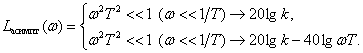
2) Идеальное интегрирующее звено:
- cтатическая характеристика - нет;
t
- уравнение движения - X(t) = X(0) + K× ò U(t)dt;
0
- передаточная функция - W(s) = K/s;
- переходная функция - H(t) = K× t;
- весовая функция - W(t) = K;
- амплитудно-частотная характеристика - А(w) = K/w;
- фазо-частотная характеристика - F(w) = - p/2;
- амплитудно-фазо-частотная характеристика - W(jw) = -jK/ w;
- логарифмическая амплитудно-частотная характеристика –
- L(w) = 20× lg(K) - 20× lg(w).
K = 1
2.1. Комплексный коэффициент передачи (ККП) идеального интегрирующего звена
W(jw) = -jK/ w= -j/ w
2.2. Выражения для АЧХ, ФЧХ, ЛАЧХ
АЧХ: А(w) = K/w = 1/ w
ФЧХ: F(w) = -K/w=- p/2
при w = 0: F(w) = - p/2,
при w < 0: F(w) = F(w) - p;
ЛАЧХ: L(w) = 20× lg(K) - 20× lg(w) = 20× lg(1) - 20× lg(w)
2.3. На рабочем поле собрал схему, состоящую из генератора ступенчатого сигнала, идеального интегрирующего звена и осциллографа, получил график переходного процесса.
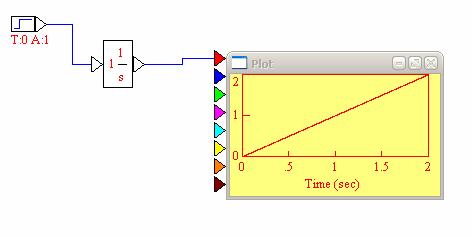
Рис. 6. Переходной процесс идеального интегрирующего звена
2.4. Построил ЛАЧХ и ЛФЧХ идеального интегрирующего звена
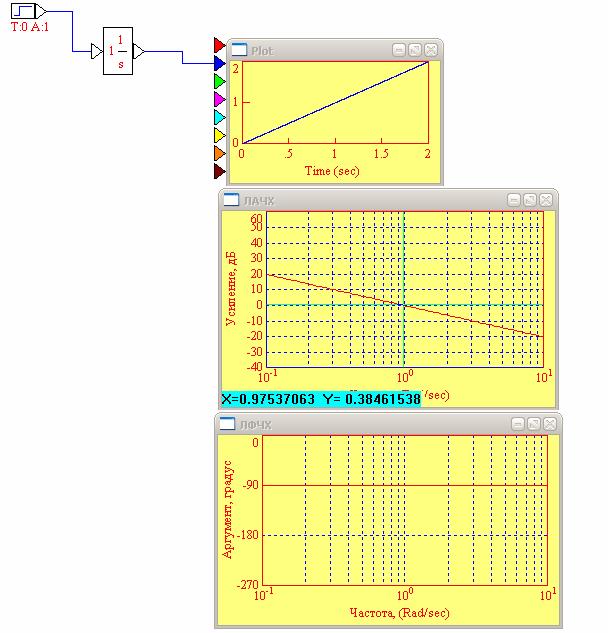
Рис. 7. ЛАЧХ и ЛФЧХ идеального интегрирующего звена при K=1
20lgK=20lg1=0
ω ср=0, 97 рад/с=1 рад/с
ω с=0 рад/с
k=100/20=1
Так как идеальное интегрирующее звено не зависит от постоянной времени, менял только значение коэффициента усиления (K=5)
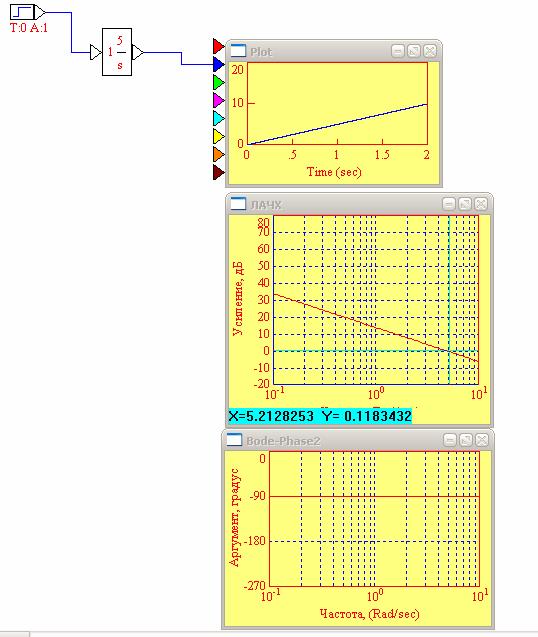
Рис. 8. ЛАЧХ и ЛФЧХ идеального интегрирующего звена при K=5
20lgK=20lg5=13.98
ω ср=5.2 рад/с
ω с=0
k=1013.98/20=5
2.4. Построил амплитудно-фазовую частотную характеристику АФЧХ (или годограф Найквиста) для идеального интегрирующего звена.
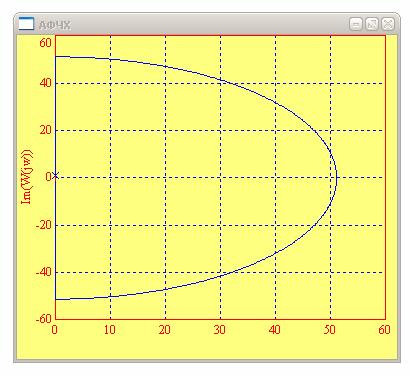
Рис. 9. АФЧХ идеального интегрирующего звена
Вывод:
В ходе исследования идеального интегрирующего звена я получил: комплексный коэффициент передачи (ККП), выражения для АЧХ, ФЧХ, ЛАЧХ, график переходного процесса(рис.6). Построил ЛАЧХ и ЛФЧХ идеального интегрирующего звена при разных вариациях коэффициента усиления. Так как идеальное интегрирующее звено не зависит от постоянной времени, то менял только коэффициент усиления. При каждой вариации по графикам определял частоту среза, частоту сопряжения и коэффициент усиления (рис. 7 – рис. 8). При изменении коэффициента усиления частота среза менялась, а частота сопряжения оставалась неизменно й, равной нулю, т.к. изображена линейная зависимость (не зависимость от постоянной времени). При всех вариациях ЛФЧХ оставалась одной и той же. Построил амплитудно-фазовую частотную характеристику АФЧХ (или годограф Найквиста) для идеального интегрирующего звена. Указал направление обхода контура (рис. 9).
3) Изодромное звено:
-передаточная функция - W(s) = K(Ts+1)/s
K=3; T=0.9
3.1. Комплексный коэффициент передачи (ККП) изодромного звена
W(jw) = KTw2 /w2 -jK w/w2 =2.7 w2 /w2 –j3 w/w2
3.2. Выражения для АЧХ, ФЧХ, ЛАЧХ
АЧХ: А(w) = K/w*(T2w2+1)1/2 = 3/w*(0.81w2+1)1/2
ФЧХ: F(w) =arctg-1/Tw=arctg-1/0.9w
ЛАЧХ: L(w) = (20× lg(K) +20 lg(T2w2+1)1/2)-20× lg(w) = (20× lg(3) +20 lg(0.81w2+1)1/2)-20× lg(w)
3.3. На рабочем поле собрал схему, состоящую из генератора ступенчатого сигнала, изодромного звена и осциллографа, получил график переходного процесса.
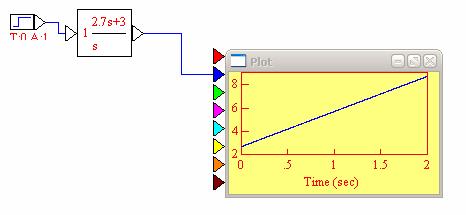
Рис. 10. Переходной процесс изодромного звена
3.4. Построил ЛАЧХ и ЛФЧХ изодромного звена
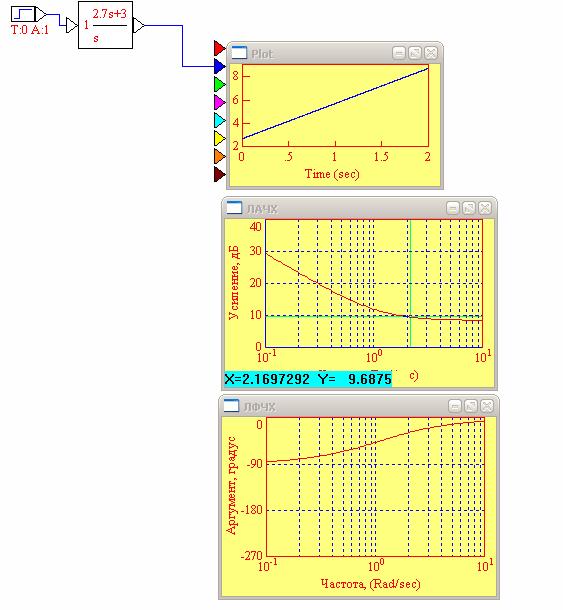
Рис. 11. ЛАЧХ и ЛФЧХ изодромного звена при T=0.9; K=3
20lgK=20lg3=9.54
ω ср= 0
ω с=2, 17 рад/с (ω c=1/T=1/0.9=1.1)
k=109.54/20=2.99≈ 3
Изменил сначала значение коэффициента усиления (K=5)
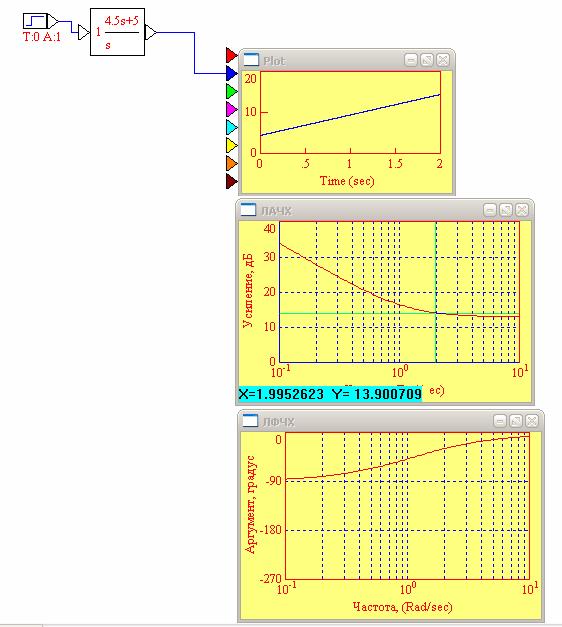
Рис. 12. ЛАЧХ и ЛФЧХ изодромного звена при T=0.9; K=5
20lgK=20lg5=13.98
ω ср= 0
ω с=1.99 рад/с (ω c=1/T=1/0.9=1.1)
k=1013.98/20=5
Изменил значение постоянной времени (T=0.5)
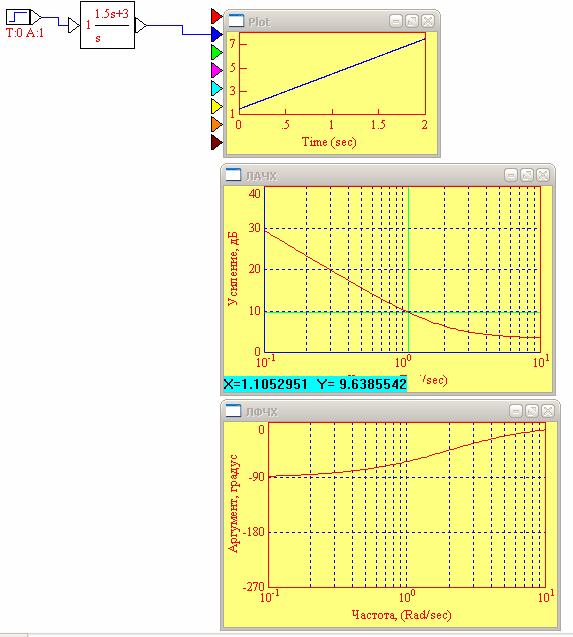
Рис. 13. ЛАЧХ и ЛФЧХ изодромного звена при T=0.5; K=3
20lgK=20lg3=9.54
ω ср= 0
ω с=1, 10 рад/с (ω c=1/T=1/0.5=2)
k=109.54/20=2.99≈ 3
3.4. Построил амплитудно-фазовую частотную характеристику АФЧХ (или годограф Найквиста) для изодромного звена.
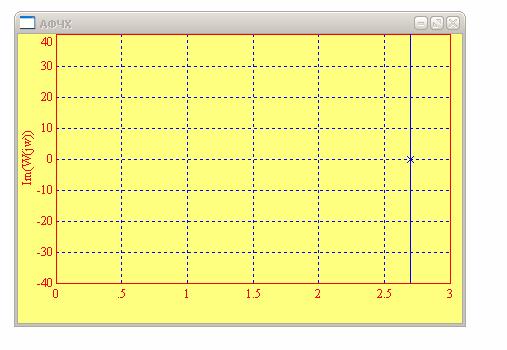
Рис. 14. АФЧХ изодромного звена
Вывод:
В ходе исследования изодромного звена я получил: комплексный коэффициент передачи (ККП), выражения для АЧХ, ФЧХ, ЛАЧХ, график переходного процесса(рис.10). Построил ЛАЧХ и ЛФЧХ изодромного звена при разных вариациях коэффициента усиления и постоянной времени. При каждой вариации по графикам определял частоту среза, частоту сопряжения и коэффициент усиления (рис. 11 – рис. 13).При всех вариациях частота среза была равна нулю, т.к. не было пересечения ЛАЧХ с осью 0дБ. При изменении постоянной времени менялась частота сопряжения. При изменении коэффициента усиления и постоянной времени частота сопряжения менялась с большим отклонением от теоретического значения. При всех вариациях ЛФЧХ оставалась одной и той же. Построил амплитудно-фазовую частотную характеристику АФЧХ (или годограф Найквиста) для изодромного звена. (рис. 14). В итоге получил вертикальную прямую линию. Асимптотическая ЛАХ представляет собой две прямые: с отрицательным наклоном 20дБ/дек (при w< 1/T) и параллельную оси частот (при w> 1/T).
4.1. Нашел выражение для передаточной функции заданного дифференциального уравнения
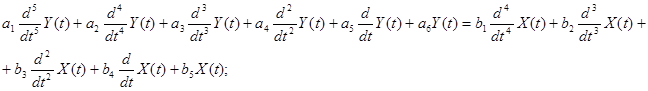
a3=8; a4=-9; a5=3; a6=4; b3=5; b4=-6; b5=4
Передаточная функция находится по формуле:
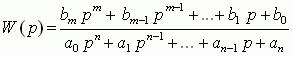
Получим следующее дифференциально уравнение:
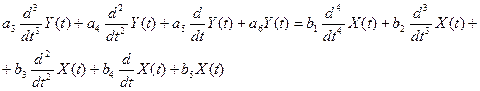
Подставим значения:
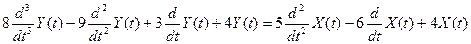
Теперь получим передаточную функцию:
W(s) = 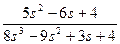
4.2. Построил ЛАЧХ, ЛФЧХ и АФЧХ для полученной передаточной функции
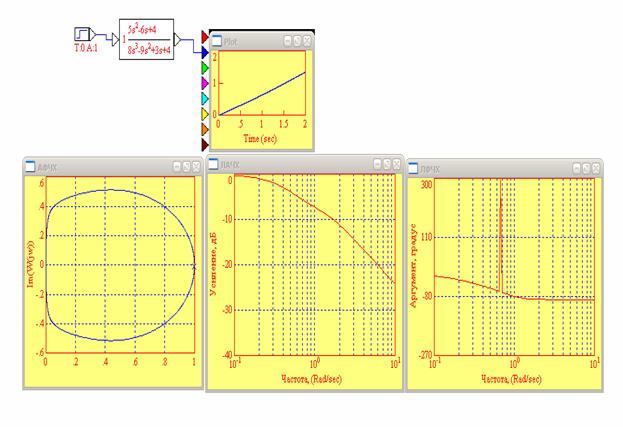
Рис.15. ЛАЧХ, ЛФЧХ, АФЧХ полученной передаточной функции
Вывод:
Получил передаточную функцию из общего вида дифференциального уравнения, подставив известные по варианту(6) коэффициенты полиномов. Изучил полученную передаточную функция. Построил ЛАЧХ, ЛФЧХ, АФЧХ полученной передаточной функции, а также построил график переходного процесса.
|