Вопрос 14. Ассиметрия и эксцесс. Z-величины.

Для проверки нормальности распределения могут применяться коэффициенты асимметрии и эксцесса, которые характеризуют отклонения формы распределения от нормальной. В случае нормального распределения оба эти коэффициента равны нулю.

Коэффициент асимметрии As вычисляется по следующей формуле:

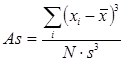
Коэффициент асимметрии характеризует скошенность распределения. Если As> 0, то левый склон распределения более крутой, а правый - более пологий (т.е. имеется несколько значений, существенно превышающих остальные). Если As< 0, то наоборот, имеется несколько значений, значительно меньших остальных.

Эксцесс характеризует пикообразность распределения. Если форма распределения пологая, то эксцесс меньше 0, а если крутая, то больше 0. Эксцесс вычисляется по формуле:

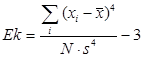
В обеих формулах s- это стандартное (стандартное) отклонение.

В качестве примера оценим асимметрию и эксцесс по выборке, которую мы использовали в рассказе о вычислении среднего значения и стандартного отклонения. Выборка состояла из следующих 12 значений: 1, 3, 0, 2, 2, 4, 1, 1, 0, 2, 2, 3.

Как видно из формул, сначала требуется вычислить выборочные среднее значение и стандартное отклонение. Их мы вычислили ранее: 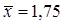, s=1, 163687. Подставляем эти данные в формулу для асимметрии и получаем:

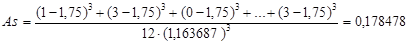
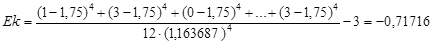
Если данные сгруппированы в виде частотной таблицы, то формулы изменятся примерно так же, как они изменялись при вычислении среднего значения и дисперсии (которые также потребуется заранее вычислить), а именно к каждому элементу суммы добавится множитель числа ответов в данной категории n_i. Формулы примут следующий вид:

,

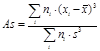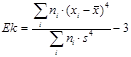
Для иллюстрации применения этих формул используем тот же пример, но с предварительно сгруппированными данными (как это уже было сделано ранее):

Ранее уже было вычислено и для такой записи данных, что 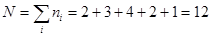, а среднее значение и стандартное отклонение по-прежнему равны, соответственно, 1.75 и 1.163687. Находим асимметрию и эксцесс:

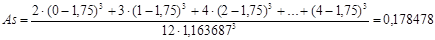
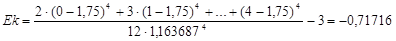
Естественно, результат получился тот же.

Предположим, значения одной величины измеряются в единицах или в десятках, а другой величины – в миллионах (такие уж единицы измерения были выбраны). Тогда значения и разброс первой величины окажутся очень малыми по сравнению со значениями и разбросом второй величины. Многие же сложные виды анализа (дисперсионный, кластерный анализ и т.п.) основаны на анализе средних значений и дисперсий. Введение нормированных величин позволяет в таких задачах обеспечить равный вклад этих факторов.

Нормировка заключается в следующей процедуре. Пусть у нас есть (одна) случайная величина x, измеряемая по интервальной шкале. Для нее имеется некоторая выборка из i значений: x₁, x₂, … x_i. Можно вычислить (оценить по этой выборке) ее среднее значение 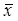и стандартное отклонение s. А теперь из каждого значения вычтем среднее значение 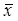, а затем полученные разности разделим на s. У нас получится i новых значений z₁, z₂, …, z_i., где 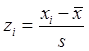. Для дальнейших вычислений возможно использовать именно эти z-величины. Среднее значение такой величины равно 0, а ее дисперсия и стандартное отклонение равны 1. Причем и сами значения, и дисперсия, и стандартное отклонение – величины безразмерные.

Пример вычисления z-величины:

Пусть у нас имелись значения: 1, 3, 0, 2, 2, 4, 1, 1, 0, 2, 2, 3. Ранее мы уже вычислили среднее значение этой величины 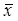=1.75 и ее стандартное отклонение s=1.163687.

Нормируем 1-е значение: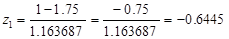

Аналогичную процедуру делаем для всех значений, и получаем новый список величин:

-0.6445, 1.074172, -1.50384, 0.214384, 0.214384, 1.93351, -0.6445 …, 1.074172

Обратите внимание, что получилось примерно равное количество положительных и отрицательных величин, а также то, что очень мало значений больше 3 и меньше -3. Именно так должно быть, если распределение близко к нормальному.

Формула для функции нормального распределения Z-величины совпадает с кривой Гаусса, для которой имеются таблицы значений (в том числе во многих учебниках). Поэтому часто при проверке гипотезы о том, является ли распределение случайной величины нормальным, сначала вычисляют для нее Z-величины, а потом уже проверяют, является ли нормальным распределение этой Z-величины.