
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Разложение рациональной дроби на простейшие
|
|
Лабораторная работа 2
ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ДРОБЕЙ
Разложение рациональной дроби на простейшие
Простейшими (элементарными) дробями называются дроби вида 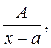
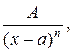
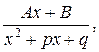
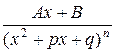
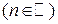 , где
, где 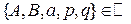 , а квадратный трехчлен
, а квадратный трехчлен 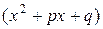 не имеет действительных корней.
не имеет действительных корней.
Дробь 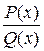 называется рациональной, если её числитель и знаменатель многочлены с действительными коэффициентами. Рациональная дробь называется правильной, если степень многочлена
называется рациональной, если её числитель и знаменатель многочлены с действительными коэффициентами. Рациональная дробь называется правильной, если степень многочлена 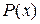 меньше, чем степень многочлена
меньше, чем степень многочлена 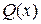 . Всякая неправильная рациональная дробь может быть представлена в виде суммы многочлена и правильной дроби, поэтому интегрирование рациональной дроби всегда может быть приведено к интегрированию многочлена и правильной дроби.
. Всякая неправильная рациональная дробь может быть представлена в виде суммы многочлена и правильной дроби, поэтому интегрирование рациональной дроби всегда может быть приведено к интегрированию многочлена и правильной дроби.
Теорема (о разложении рациональной дроби на простейшие).
Пусть 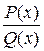 - правильная, несократимая рациональная дробь, а её знаменатель после разложения на множители имеет вид:
- правильная, несократимая рациональная дробь, а её знаменатель после разложения на множители имеет вид:
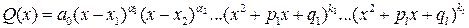 ,
,
где 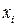 – действительные числа, а квадратичные множители не имеют действительных корней. Тогда дробь
– действительные числа, а квадратичные множители не имеют действительных корней. Тогда дробь 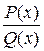 может быть представлена в виде суммы простейших дробей. В этой сумме каждому множителю вида
может быть представлена в виде суммы простейших дробей. В этой сумме каждому множителю вида 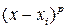 в знаменателе соответствует выражение вида
в знаменателе соответствует выражение вида
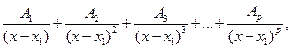
а каждому множителю 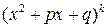 знаменателя – выражение вида
знаменателя – выражение вида
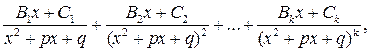
где 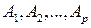 ,
, 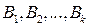 ,
, 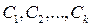 – некоторые действительные коэффициенты.
– некоторые действительные коэффициенты.
Пример. 1) 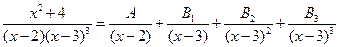 ;
;
2) 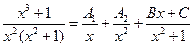 .
.
Для нахождения неопределенных коэффициентов 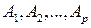 ,
, 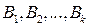 ,
, 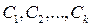 можно применять метод неопределенных коэффициентов.
можно применять метод неопределенных коэффициентов.
Пример. Разложить на простейшие дроби рациональную дробь 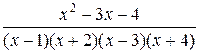 .
.
Решение.
Общий вид разложения будет таким:
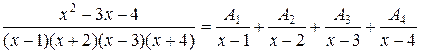
Для нахождения коэффициентов применим метод неопределённых коэффициентов.
1) Приведем правую часть этого равенства к общему знаменателю 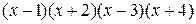 , в результате получим тождество
, в результате получим тождество
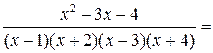
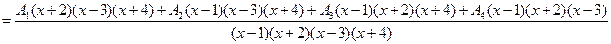 .
.
2) Так как в полученном тождестве знаменатели равны, то тождественно равны и числители:
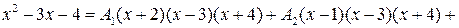
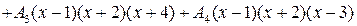 . (*)
. (*)
3) В правой части произведём умножение двучленов и получим: 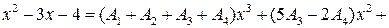
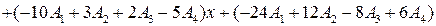
Приравнивая коэффициенты при одинаковых степенях x в обеих частях тождества (*), получаем систему четырёх уравнений первой степени с четырьмя неизвестными:
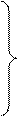
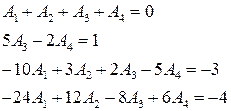
Решая систему, находим, что 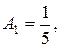
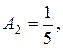
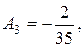
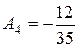 .
.
Теперь определим числа 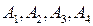 вторым способом – способом задания частных значений. Так как равенство (*) тождество, то оно сохраняется при любом значении x. Будем задавать такие значения x, чтобы в правой части все члены, кроме одного, обращались в нуль. Такими выгодными значениями являются, очевидно, корни знаменателя, т.е. значения
вторым способом – способом задания частных значений. Так как равенство (*) тождество, то оно сохраняется при любом значении x. Будем задавать такие значения x, чтобы в правой части все члены, кроме одного, обращались в нуль. Такими выгодными значениями являются, очевидно, корни знаменателя, т.е. значения 
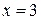 ,
, 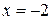 ,
, 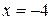 . При
. При 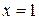 в правой части (*) все слагаемые, кроме первого обратятся в нуль, левая часть будет равна –6, и мы получим
в правой части (*) все слагаемые, кроме первого обратятся в нуль, левая часть будет равна –6, и мы получим
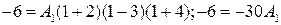 ;
; 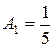 .
.
Аналогично при 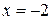 левая часть равна 6, а в правой части все слагаемые, кроме второго, будут равны нулю:
левая часть равна 6, а в правой части все слагаемые, кроме второго, будут равны нулю: 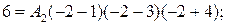
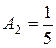
При 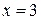 :
: 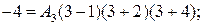
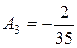
При 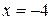 :
: 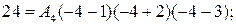
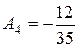
Заметим, что каким бы способом ни вычислялись неизвестные коэффициенты, мы всегда получим для них одни и те же значения, т.к. разложение на простейшие дроби может быть осуществлено единственным образом. Итак, заданная дробь
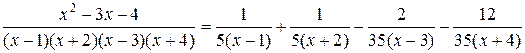 .
.
1.1 Разложить на простейшие дроби следующие рациональные дроби
1 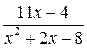 ; 6
; 6 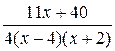 ;
;
2 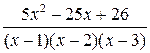 ; 7
; 7 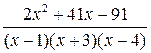 ;
;
3 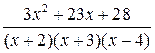 ; 8
; 8 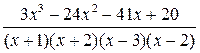 ;
;
4 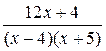 ; 9
; 9 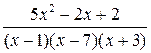 ;
;
5 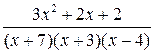 ; 10
; 10 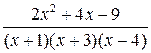 .
.
1.2 Разложите на простейшие дроби рациональную дробь:
1  ; 6
; 6 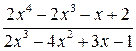 ;
;
2 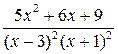 ; 7
; 7 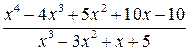 ;
;
3 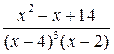 ; 8
; 8 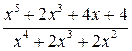 ;
;
4 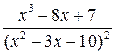 ; 9
; 9 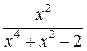 ;
;
5 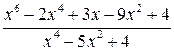 ; 10
; 10 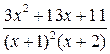 .
.