
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Интегрирование простейших рациональных дробей
|
|
Рассмотрим методы вычисления интегралов от простейших рациональных дробей.
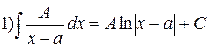 ;
;
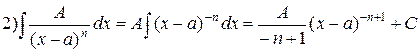 ;
;
3) 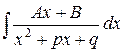
Данный интеграл вычисляется следующим образом: в числителе дроби, стоящей под интегралом, записывается производная знаменателя, т.е. 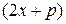 . Тождественными преобразованиями из
. Тождественными преобразованиями из 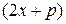 получают заданный числитель
получают заданный числитель 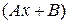 . Для этого следует
. Для этого следует 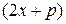 умножить на
умножить на  и к полученному произведению прибавить
и к полученному произведению прибавить 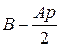 . Очевидно, что
. Очевидно, что 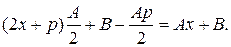
Преобразованная дробь 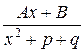 имеет вид:
имеет вид:
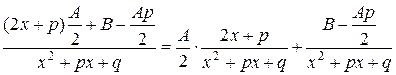
Первая дробь интегрируется методом поднесения переменного множителя под знак дифференциала, что приводит к натуральному логарифму модуля знаменателя.
Для интегрирования второй дроби в знаменателе выделяют полный квадрат:
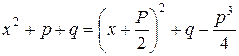
Интеграл второй дроби приводится к табличному интегралу
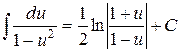 , если
, если 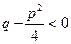 .
.
Если в знаменателе дроби вместо трёхчлена x2+px+q стоит трёхчлен ax2+bx+c (a≠ 0), то коэффициент a выносится за скобку и данный случай сводится к предыдущему.
2.1 Вычислить интегралы:
1 а) 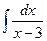 ; б)
; б) 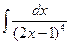 ; в)
; в) 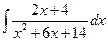 .
.
2 а) 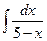 ; б)
; б) 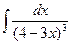 ; в)
; в) 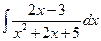 .
.
3 а) 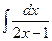 ; б)
; б) 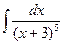 ; в)
; в) 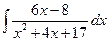 .
.
4 а) 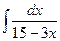 ; б)
; б) 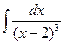 ; в)
; в) 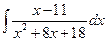 .
.
5 а) 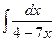 ; б)
; б) 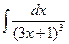 ; в)
; в) 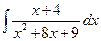 .
.
6 а) 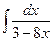 ; б)
; б) 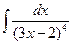 ; в)
; в) 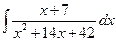 .
.
7 а) 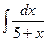 ; б)
; б) 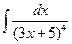 ; в)
; в) 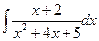 .
.
8 а) 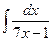 ; б)
; б) 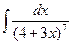 ; в)
; в) 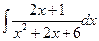 .
.
9 а) 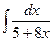 ; б)
; б) 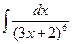 ; в)
; в) 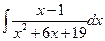 .
.
10 а)  ; б)
; б) 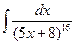 ; в)
; в) 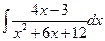 .
.
4) Интеграл вида 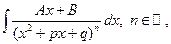 где знаменатель не имеет действительных корней, сводится к вычислению двух интегралов. Это достигается следующим образом: в числителе записывается производная основания степени знаменателя, т.е. (x2+px+q)' = 2x+p и так же, как в предыдущем пункте, эта производная преобразовывается в выражение Ax+B, стоящее в числителе:
где знаменатель не имеет действительных корней, сводится к вычислению двух интегралов. Это достигается следующим образом: в числителе записывается производная основания степени знаменателя, т.е. (x2+px+q)' = 2x+p и так же, как в предыдущем пункте, эта производная преобразовывается в выражение Ax+B, стоящее в числителе:
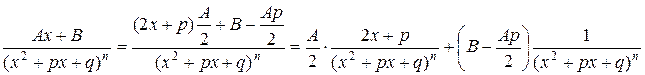
Интегрирование первой дроби описано в пункте 3. Рассмотрим вторую дробь
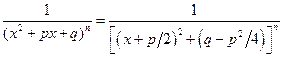 . Если обозначить
. Если обозначить 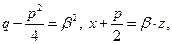 то
то
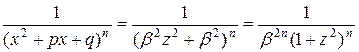 и таким образом интегрирование второй дроби в правой части сводится к интегрированию дроби
и таким образом интегрирование второй дроби в правой части сводится к интегрированию дроби 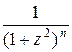 . Интеграл
. Интеграл 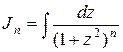 вычисляется по формуле
вычисляется по формуле
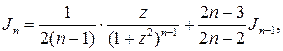 где
где 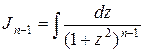 . Данная формула дает возможность найти интеграл
. Данная формула дает возможность найти интеграл 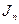 для любого натурального
для любого натурального 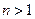 .
.
2.2 Вычислить интегралы
1 а) 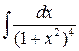 ; б)
; б) 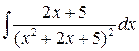 ;
;
2 а) 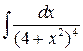 ; б)
; б) 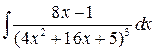 ;
;
3 а) 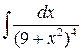 ; б)
; б) 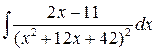 ;
;
4 а) 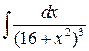 ; б)
; б) 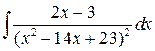 ;
;
5 а) 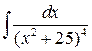 ; б)
; б) 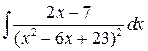 ;
;
6 а) 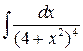 ; б)
; б) 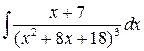 ;
;
7 а) 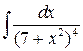 ; б)
; б) 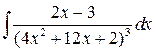 ;
;
8 а) 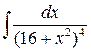 ; б)
; б) 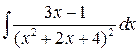 ;
;
9 а) 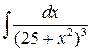 ; б)
; б) 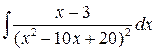 ;
;
10 а) 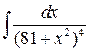 ; б)
; б)  .
.