Разложение вектора по системе векторов.

В задачах, где рассматриваются геометрические векторы, бывает важным выяснить, являются ли векторы компланарными, т.е лежат ли они в одной и той же плоскости.

Если все векторы лежат в одной плоскости, то речь идет о плоской задаче. Если они не лежат в одной и той же плоскости, то рассматривается стереометрическая задача.

Рассмотрим три трехмерных вектора 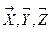лежащих в одной плоскости. В этом случае один из них можно разложить по направлению двух других.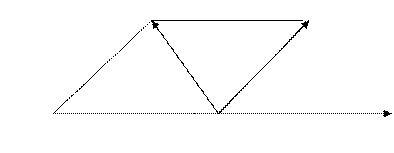

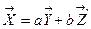, a, b - числовые множители.

Определение. Векторы называются линейно зависимыми, если существуют такие не все равные нулю числа 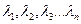, что выполняется равенство: 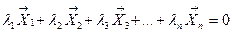(3.2.1)

В развернутом виде:

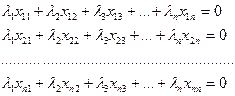
Если равенство (3.2.1) выполняется только тогда, когда все 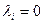, то 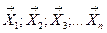называются линейно независимыми.

Содержательно линейная зависимость совокупности векторов означает, что в ней имеются «лишние векторы». Эти «лишние векторы» не несут информации, которая не могла бы быть получена из всех векторов совокупности, состоящей только из линейно независимых векторов.

Теорема Для того, чтобы векторы 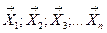были линейно зависимы, необходимо и достаточно, чтобы хотя бы один из них являлся линейной комбинацией других.

Теорема Для того, чтобы векторы 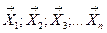в пространстве Rⁿ были линейно независимы, необходимо и достаточно, чтобы определитель составленный из компонент этих векторов был отличен от нуля.

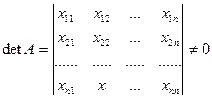
Пример Дана система векторов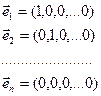

Линейно зависимы или линейно независимы эти векторы?

Решение: 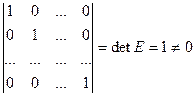, векторы линейно независимы.