Математические модели динамических систем.

Рассмотрим математическую модель системы в самой общей форме.

В начале остановимся на некоторых предложениях о функционировании системы.

1. Любая система функционирует во времени.

2. В любой момент времени система находится в одном из возможных состояний.

Пример:

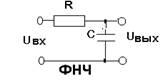Рис. 2.2

1. Система передачи информации 2. Фильтр нижних частот

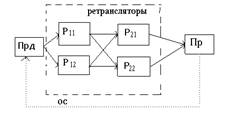Рис. 2.1

Состояние СПИ определяется нахождением сообщения в момент времени t, например в P₂₁

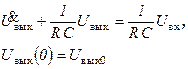
Состояние ФНЧ в момент времени t определяется значением U (t) Обозначим существенные параметры системы через 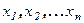. Тогда состояние системы может быть описано вектором состояния:

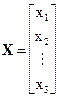для СПИ 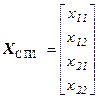; для ФНЧ .

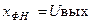Все возможные состояния модели системы 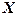образуют пространство состояний или фазовое пространство.

Например для n=3

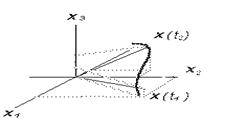Рис. 2.3

При изменении t в фазовом пространстве образуется траектория, которая называется фазовой. (Конец вектора состояния прочерчивает траекторию).

Введем определение для динамической системы:

Динамической системой называется такая система, которая в течение интервала времени функционирования переходит от одного состояния к другому.

Если система не меняет со временем своего состояния, то она называется статической.

Значения, которые могут принимать элементы вектора состояния образуют область допустимыхзначений (ОДЗ).

3. Изменения состояния системы и происходит под влиянием как внешних так и внутренних воздействий.

Внешние воздействия обусловлены воздействием среды на систему и является входным.

Входные воздействия: - управляющие;

- возмущающие.

Управляющие воздействия это такие, которые целенаправленно изменяют состояние системы.

Управляющие воздействия можно представить в виде вектора: .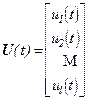

Возмущающие воздействия это такие, которые изменяют состояние системы случайным, непредсказуемым образом.

Также можно представить вектором 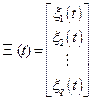кси

4. Система, изменяя свое состояние, в свою очередь оказывает влияние на окружающую среду.

Это влияние проявляется в виде выходных воздействий .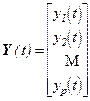

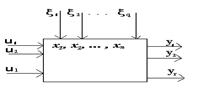Рис. 2.4

Эквивалентная схема динамической системы:

Последовательность изменения состояний системы во времени называется движением системы.

Уравнение, описывающее состояние системы, называется уравнением состояния.

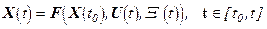
Виды уравнений: - непрерывные;

-?

- дифференциальные;

- дискретные;

-?

- конечно-разностные.

Изменение состояния системы ведет к изменению выходного воздействия, которое описывается уравнением выхода.

Записанные уравнения относятся к классу стохастических.

Если 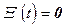, то система и соответствующие уравнения - детерминированные.