
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Постановка задачи параметрического программирования
|
|
Постановка задачи параметрического программирования геометрический подход к решению
Геометрическая интерпретация задачи параметрического программирования
Аналитический метод решения задач параметрического программирования
Постановка задачи параметрического программирования
Задачи ПП являются обобщением задач ЛП. Это обобщение состоит в том, что исходная информация ЗПП не является статической (постоянной) в течение решения всей задачи, а динамически (в данном случае линейно) изменяется в зависимости от некоторого параметра.
Если предположить, например, что произведенная предприятием продукция подлежит предварительному хранению, то ее стоимость будет складываться из двух частей:
- постоянной – стоимость продукции на момент изготовления;
- переменной – стоимость, зависящая от срока хранения.
В этом случае целевая функция, отражающая тем или иным способом стоимость произведенной продукции, будет выражена через коэффициенты, линейно зависящие от параметра (в данном примере от времени t).
Кроме того, на практике часто встречаются задачи, в которых значения коэффициентов ЦФ известны только приближенно. Представив эти коэффициенты в виде линейных функция от некоторого параметра(например, времени) можно проанализировать изменение результата решения задачи при различных значениях этих коэффициентов.
Аналогично можно рассуждать и о функциях ограничениях, в которых некоторые или все коэффициенты могут быть зависимыми от какого либо параметра.
В данной лекции мы будем рассматривать только такие задачи параметрического программирования, в которых зависимыми являются только коэффициенты в целевой функции.
Сформулируем постановку такой задачи:
Пусть задана целевая функция вида
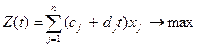 , (17.1)
, (17.1)
в которой коэффициенты при переменных xj линейно зависят от параметра t, причем 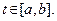 .
.
В системе ограничений параметры остаются неизменными:
 (17.2)
(17.2)
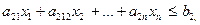
…………………………..
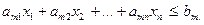
Заданы также стандартные ограничения 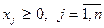 .
.
В данном случае, определить одноэтапно оптимальный план не представляется возможным, т.к. он может изменяться в зависимости от изменения параметра t.
Поэтому задача формулируется следующим образом:
- разбив общий интервал изменения параметра 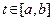 , необходимо вычислить значения переменных xj, при которых ЦФ приобретает максимум (минимум) в одной в одной и той же вершине многогранника решений на некотором очень малом интервале изменения параметра t.
, необходимо вычислить значения переменных xj, при которых ЦФ приобретает максимум (минимум) в одной в одной и той же вершине многогранника решений на некотором очень малом интервале изменения параметра t.