
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Геометрическая интерпретация задачи параметрического программирования
|
|
Геометрическая интерпретация такой задачи может быть представлена следующим образом.
Положим t = α и ограничимся только двумя переменными x1 и x2. В этом случае получаем стандартную задачу ЛП (рисунок 17.1). Решение этой задачи – точка в вершине А многогранника решений.
Рисунок 17.1 – Геометрическая интерпретация задачи
Если теперь изменить значение t (t1 = α 1), то это будет математически соответствовать изменениям коэффициентов целевой функции, а геометрически – повороту вектора градиента этой функции на некоторый угол (на рисунке 17.1 – переход от прямой Zα к прямой Zα 1 ). В этом случае происходит и изменение решения задачи. Теперь оно будет находиться в вершине многогранника решений А1 .
Естественно предположить, что при некотором t2 < α 1, решение будет находиться в обоих точках А и А1, а следовательно и в любой точке отрезка, соединяющего эти точки (прямая соответствующая целевой функции параллельна стороне многогранника А-А1.).
Фиксированное значение t1 является граничной точкой между двумя соседними интервалами отрезка [ab].
Такой подход позволяет решить задачу параметрического программирования с двумя переменными графическим методом.
Пример 17.1. Задана целевая функция вида
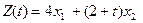 , (17.3)
, (17.3)
где 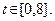 (17.4)
(17.4)
Система ограничений неравенств имеет вид
2х1 – 5х2 ≤ 10, (17.5)
х1 + х2 ≥ 5,
-х1 – х2 ≤ 4,
4х1 + 5х2 ≤ 40.
х1, х2 ≥ 0.