
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решение. Положим t = 0 (нижнее значение интервала изменения t) .
|
|
Положим t = 0 (нижнее значение интервала изменения t).
Решим графически задачу при этом значении параметра t.
Рисунок 17.2 – Решение задачи ПП графическим методом
Как следует из рисунка 17.2, решение задачи при t = 0 находится в точке С.
Далее приравняем нулю Z(t) и получим уравнение разрешающей прямой при любом t
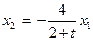 . (17.6)
. (17.6)
Введем обозначение углового коэффициента прямой
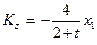 .
.
Рассчитаем значение коэффициента при t = 0 → Kz = -2.
Вычислим производную от Кz по параметру t
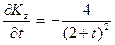 . (17.7)
. (17.7)
Из анализа (17.7) следует, что производная отрицательна при любых значениях t и возрастает при изменении t от со стороны (-∞) до 0, и следовательно, разрешающая прямая поворачивается против часовой стрелки до предельного горизонтального положения. При этом необходимо понимать, что при вертикальном положении прямой угловой коэффициент как функция терпит разрыв.
При вращении прямой против часовой стрелки от оси абсцисс до вертикального положения угловой коэффициент возрастает от 0 до + ∞, а при дальнейшем вращении прямой в – возрастает от (-∞) до 0.
В данном примере при изменении параметра мt от нуля до некоторого значения максимальное значение ЦФ будет в вершине С, затем в некоторый фиксированный момент времени оптимум будет достигаться на отрезке ВС, а затем он перейдет в точку В и останется в ней для всех значений t отрезка [0, 8].
Определим значение t, при котором Zmax будет соответствовать всем точкам отрезка ВС.
Поскольку в этот момент прямая ВС и разрешающая прямая должны быть параллельны, приравняем их угловые коэффициенты.
Угловой коэффициент прямой ВС - КВС = - 4/5, следовательно
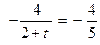 .
.
Откуда t = 3.
Таким образом:
- при 0 ≤ t < 3 оптимальное решение – вершина С(8, 3; 1, 3);
- при t = 3 – оптимальное решение достигается в любой точке отрезка ВС;
- при 3 < t ≤ 8 - оптимальное решение – вершина B(2, 2; 6, 2).