
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Перевод целых чисел
|
|
Правило перевода методом последовательного деления на основание
Чтобы перевести целое число из десятичной системы счисления в систему счисления по основанию p, необходимо:
Шаг 1: Разделить исходное десятичное число на основание системы счисления p. В результате деления получается промежуточное частное и остаток от деления.
Шаг 2: Если полученное промежуточное частное больше делителя, то процесс деления продолжается (переход на шаг 1), а если меньше, то переход на шаг 3.
Шаг 3: Последнее частное и полученные остатки дают искомое изображение р -ичного числа, причем первый остаток записывается в младший разряд, а последнее частное – в старший разряд числа.
Пример №6. Перевести число Х=8410 в восьмеричную систему счисления.
Для перевода числа 8410 в восьмеричную систему счисления воспользуемся методом деления на основание. Для этого:
Число 84 делим на основание системы счисления - 8, в результате получается частное (в данном случае 10) и остаток от деления (в данном случае 4). Промежуточное частное больше 8 поэтому продолжаем процесс деления (см. рис.1).
Второе промежуточное частное получилось равное 1, а остаток от деления равный 2. Процесс деления заканчивается, т.к. частное меньше делителя. Запись восьмеричного числа осуществляется с последнего промежуточного частного (в данном случае 1), эта цифра является старшим разрядом искомого числа. Следующим за старшим разрядом следуют остатки от деления (в данном случае 2 и 4). В результате получается искомое число 1248.
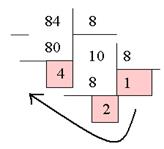
Рис.1 Пример деления исходного числа на основание системы счисления 8.
Ответ: Х= 8410=1248
Пример №7. Перевести число Х=34510 в шестнадцатеричную систему счисления.
Для перевода числа 34510 в шестнадцатеричную систему счисления воспользуемся методом деления на основание. Для этого необходимо число 345 разделить на основание системы счисления, т.е. на 16, до тех пор, пока целая часть частного не окажется меньше делителя (см. рис.2.).

Рис.2 Пример деления исходного числа на основание системы счисления 16.
Запись шестнадцатеричного числа осуществляется с конца, в данном случае с 1
Ответ: Х= 34510=15916
Пример №8. Перевести число Х=1910 в двоичную систему счисления.
Для перевода числа 1910 в двоичную систему счисления воспользуемся методом деления на основание. Для этого необходимо число 19 разделить на основание системы счисления, т.е. на 2, до тех пор, пока целая часть частного не окажется меньше делителя (см. рис.3).
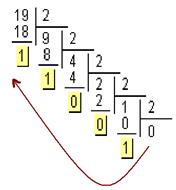
Рис.3 Пример деления исходного числа на основание системы счисления 2.
Запись двоичного числа осуществляется с конца, в данном случае с 1
Ответ: Х= 1910=100112
Пример №9. Перевести число Х=13210 в пятеричную систему счисления.
Для этого необходимо число 132 разделить на основание системы счисления, т.е. на 5, до тех пор, пока целая часть частного не окажется меньше делителя (см. рис.4).
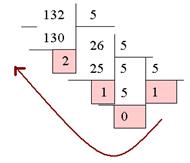
Рис.4 Пример деления исходного числа на основание системы счисления 5.
Запись пятеричного числа осуществляется с конца, в данном случае с 1
Ответ: Х= 13210=10125