
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Перевод чисел в системах счисления с основаниями кратными двум
|
|
В этом параграфе мы освоим быстрый перевод чисел, основание которых кратно двум 2= 21, 4 = 22, 8 = 23, 16 = 24 и т.д.
В случае, когда происходит перевод чисел с одним кратным основанием в другое кратное основание, процесс перевода заменяется кодировкой. В системе счисления с основанием 4 для записи чисел используется 4 символа {0, 1, 2, 3}, которые можно закодировать двумя разрядами (см.рис.7).
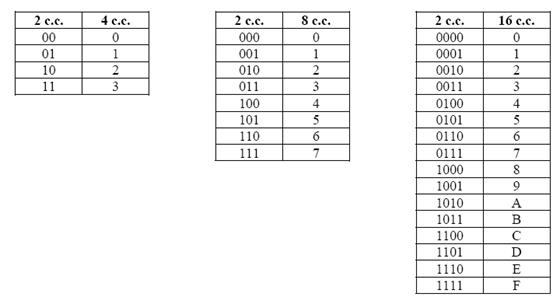
Рис.7. Таблицы соответствия двоичных чисел и чисел в системах счисления по основанию 4, 8, 16.
Если мы работаем с восьмеричной системой счисления, то кодировка осуществляется с помощью триад. Кодирование символов {0, 1, 2, 3, 4, 5, 6, 7} в системе счисления по основанию 8 представлено на рисунке 7.
Кодировка шестнадцати символов {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F} осуществляется с помощью тетрад.
При кодировании символов с помощью тетрад и триад, необходимо выполнить переход в систему счисления по основанию 2. Этот процесс можно отразить в виде схемы (см. рис.8). Данная схема поясняет, что перевод в системы счисления с основаниями кратными двум выполняется через двоичную систему счисления.
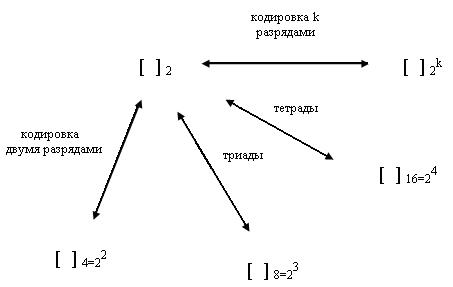
Рис.8. Схема перевода чисел в системы счисления с основаниями кратными двум.
Процедура перевода через двоичные триады:
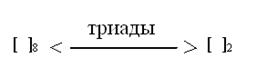
1. Исходное десятичное число перевести в двоичную систему счисления
Разбить двоичное число на группы, состоящие из трех двоичных разрядов (триады) осуществляя разбивку вправо и влево от запятой. Если крайние триады окажутся неполными, их следует дополнить нулями.
2. Каждой триаде ставится соответствующий ей восьмеричный символ (см. рис.7).
Процедура перевода через двоичные тетрады:
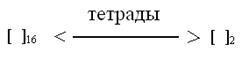
1. Исходное десятичное число перевести в двоичную систему счисления
Разбить двоичное число на группы, состоящие из четырех двоичных разрядов (тетрады) осуществляя разбивку вправо и влево от запятой. Если крайние тетрады окажутся неполными, их следует дополнить нулями.
2. Каждой тетраде ставится соответствующий ей шестнадцатеричный символ (см. рис.7).
Например, если необходимо перевести из системы счисления по основанию 16 в четверичную систему счисления, то необходимо выполнить действия отмеченные пунктиром на рисунке 9.
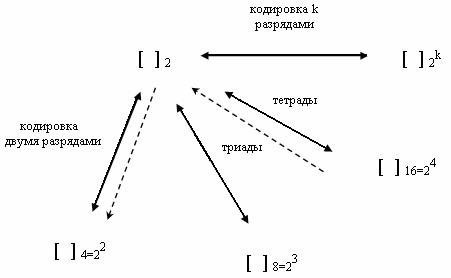
Рис.9. Схема перевода чисел из шестнадцатеричной системы счисления в четверичную.
Рассмотрим следующие примеры.
Пример №12. Перевести число Х= 4F716 в четверичную систему счисления. Для решения данного примера воспользуемся схемой перевода на рисунке 9.
Запишем число Х= 4F716 в двоичной системе счисления, для этого каждый разряд числа Х= 4F716 представим в двоичном коде, а затем полученное двоичное число разобьем на группы состоящие из двух разрядов и каждой группе определим соответствующий ей четвертичный символ.
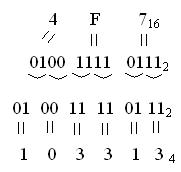
Ответ: Х=4F716= 1033134
Пример №13. Перевести шестнадцатеричное число Х= 1А57F16 в восьмеричную систему счисления.
Для решения воспользуемся схемой перевода на рисунке 9.
Перевод шестнадцатеричного числа в восьмеричное будем осуществлять через двоичные триады и тетрады.
Запишем число Х= 1А57F16 в двоичной системе счисления, для этого каждый разряд числа Х= 1А57F16 представим в двоичном коде, а затем полученное двоичное число разобьем на триады и каждой триаде определим соответствующий ей восьмеричный символ.
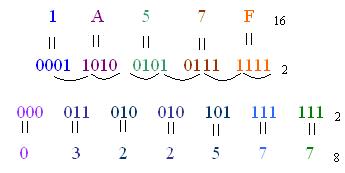
Ответ: Х= 1А57F16 = 3225778
Пример №14. Перевести число Х= 13224 в восьмеричную систему счисления.
Для решения воспользуемся схемой перевода на рисунке 9. Запишем число Х= 13224 в двоичной системе счисления, для этого каждый разряд числа Х= 13224 представим в двоичном коде, а затем полученное двоичное число разобьем на триады и каждой триаде определим соответствующий ей восьмеричный символ.
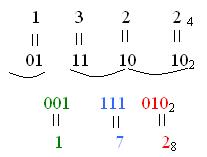
Ответ: Х= 13224 = 1728